기술

시작하려면 게임의 기본 규칙을 검토해 보겠습니다:

이 첫 번째 강의에서는 스도쿠를 푸는 데 유용한 몇 가지 팁을 제시합니다.

1. 연필을 사용하세요:컴퓨터 화면보다 연필로 스도쿠를 하는 것이 훨씬 편안합니다. 또한 연필을 사용하면 간단한 방법으로 지울 수 있습니다.
2. 점진적으로 연습하세요:일반적으로 많은 신문과 잡지는 난이도에 따라 스도쿠를 분류하지 않으므로 초보자에게는 복잡한 스도쿠를 완성하기가 정말 복잡할 수 있습니다. PrintSudoku.com에서는 스도쿠를 분류하여 귀하의 수준에 맞는 스도쿠로 연습할 수 있도록 합니다. 레벨이 높을수록 숫자를 배치하기가 더 어려워지며(일반적으로), 매우 어려운 경우에는 때때로 이동을 시도해야 합니다.
3. 이동을 시도하려면 셀의 왼쪽 상단 모서리에 후보 숫자를 쓰는 것보다 더 좋은 것은 없습니다. 작게 또는 여백에 쓰면 숫자를 제거할 때 줄을 긋습니다.
4. 천천히 하세요:스도쿠는 편안한 게임입니다. 일부 스도쿠는 몇 분 안에 풀 수 있지만 다른 스도쿠는 몇 시간 또는 며칠이 걸릴 수 있습니다.
5. 잘 설계된 스도쿠는 단 하나의 해결책만 가지고 있으며, 이 기능을 유리하게 사용하세요.
6. 가능한 모든 이동을 신중하게 검토하기 전에는 절대 시도하지 마십시오.
7. 순서를 따르세요:숫자를 배치할 때 좋은 전술은 가장 자주 나타나는 숫자부터 시작하여 가장 적게 나타나는 숫자로 끝나는 것입니다. 동점인 경우 순서를 결정하고 게임 내내 따르십시오.
8. 당신이 취하는 모든 단계가 유효한지 확인하십시오. 처음의 실수는 재앙이 될 수 있습니다.
9. 가능한 해결책을 찾을 수 없으면 도움을 요청하거나 다른 시간에 스도쿠를 시도하십시오. 많은 경우 해결책은 가장 기대하지 않을 때 나타나며, 항상 스도쿠 앞에 있을 때 나타나는 것은 아닙니다. 😉

숫자를 발견하는 가장 쉬운 방법은 행, 열 또는 사분면에 배치할 숫자가 하나만 남았을 때입니다. 이 경우 누락된 숫자는 유일한 빈 셀로 들어갑니다.

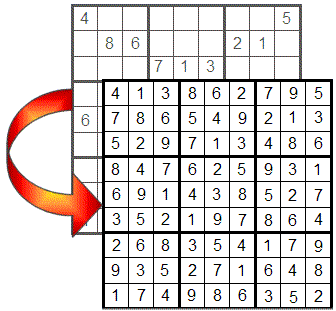
보시다시피 첫 번째 행에는 7을 제외한 모든 숫자가 배치되어 있으므로 빈 셀에는 이 숫자만 있을 수 있습니다. 첫 번째 열에서는 5와 비슷한 일이 발생하며, 여섯 번째 사분면에서는 1과 같습니다.

숫자를 발견하는 또 다른 방법은 행과 열을 교차하는 것입니다. 이것은 한 셀에 주의를 집중하고 해당 위치에 어떤 숫자가 있을 수 있는지 확인하고, 동일한 행이나 열에 있는 숫자를 제거하는 것으로 구성됩니다.

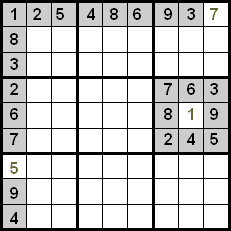
다음 이미지에서 지정된 셀에는 7만 있을 수 있음을 알 수 있습니다. 왜냐하면 1, 8, 3, 6, 9 숫자는 동일한 열에 있고 2, 4, 5 숫자는 동일한 행에 있기 때문입니다.

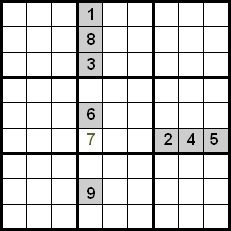
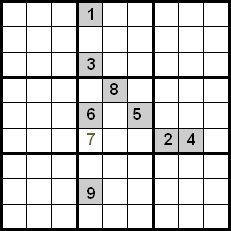
이 기술의 개선은 동일한 사분면에 있는 숫자를 제어함으로써 달성됩니다. 다음 예에서 행과 열 사이의 교차를 사용하여 표시된 셀에 배치할 5, 7, 8 숫자를 후보로 가질 수 있음을 알 수 있습니다. 5와 8 숫자는 이미 사분면 내의 위치에 배치되어 있으므로 제외할 수 있으므로 7이 지정된 위치를 차지하는 숫자입니다.

황새치(Swordfish) 기술은 특정 숫자가 정확히 세 개의 행과 세 개의 열에서 가능한 것으로 나타날 때 스도쿠에서 사용됩니다.

이 방법은 고급 게임에서 막힌 상황을 해결하는 데 특히 유용합니다. 실제 사례에서 1, 4, 7 행에서 5라는 숫자가 동일한 세 개의 열에만 갈 수 있음을 관찰하면 황새치를 식별한 것입니다. 이제 다른 모든 행의 2, 5, 8 열에서 5라는 숫자를 안전하게 제거할 수 있으며, 이는 종종 여러 셀을 지우고 나머지 스도쿠의 해결을 용이하게 합니다.

XYZ-윙은 연결을 형성하는 세 개의 셀을 찾는 데 중점을 둡니다. 여기서 두 개는 두 개의 가능한 숫자를 가지고 있고 세 번째(피벗)는 다른 두 개 각각과 숫자를 공유합니다.

실제로 스도쿠 게임에서 이 구성을 찾으면 가능성을 크게 줄일 수 있는 기회가 열립니다. XYZ-윙 기술을 적용하면 전략적으로 옵션을 제거하여 퍼즐의 더 복잡한 부분을 해결하기가 더 쉬워집니다.

이중 연결(Dual Linking) 기술은 두 개의 숫자가 행, 열 또는 블록의 두 셀에만 갈 수 있고 이 셀에 다른 숫자가 포함되어 있지 않을 때 적용됩니다.

특정 행에서 A2와 A8 셀에만 3과 7이라는 숫자가 포함될 수 있는 스도쿠를 상상해 보십시오. A2에 3이 포함되어야 한다고 해결하면 A8에 7이 포함되어야 함을 자동으로 알 수 있습니다.

상자 라인 축소(Box Line Reduction) 기술은 행이나 열에 있는 숫자의 가능한 위치가 완전히 단일 영역이나 상자 내에 있을 때 사용되는 고급 전략입니다.

예를 들어, 위쪽 상자에서 4라는 숫자가 2행의 일부인 셀에만 나타날 수 있다면 해당 상자의 다른 셀에서 4를 가능성으로 제거할 수 있습니다. 이 기술은 복잡한 스도쿠를 풀 때 효율성을 향상시킵니다.