Lessons

To begin, let's review the basic rules of the game:

In this first lesson we will present some useful tips for solving sudokus.

1. Use a pencil:It is much more comfortable to do a sudoku with a pencil than on a computer screen. In addition, the pencil allows you to erase it easily.
2. Practice gradually:Usually many newspapers and magazines do not categorize sudokus by difficulty, so for a novice, it can be really difficult to finish a complex sudoku. At PrintSudoku.com we categorize sudokus so that you can practice with sudokus according to your level. The higher the level, the more difficult it will be (usually) to place the numbers and, in the case of very difficult ones, sometimes you will have to guess moves.
3. To guess moves, there is nothing better than writing the candidate numbers in the upper left corner of the cell. If you write small or in a margin, as you discard numbers, cross them out.
4. Take it easy:Sudoku is a relaxing game. Some sudokus can be solved in a matter of minutes but others may take hours or perhaps days.
5. Well-designed sudokus have a unique solution, use this feature to your advantage.
6. Never guess until you have carefully examined all possible moves.
7. Follow an order:In the placement of numbers, a good tactic is to start with the numbers that appear most frequently, ending with the least frequent; in case of ties, decide the order and follow it throughout the game.
8. Check that each step you take is valid, a mistake at the beginning can be disastrous.
9. If you cannot find a possible solution, ask for help, or try the sudoku at another time. Often the solution appears when you least expect it, and not always when you are in front of the sudoku. 😉

The simplest way to discover a number is when in a row, column or quadrant there is only one number left to place. In this case the missing number goes in the only empty cell.

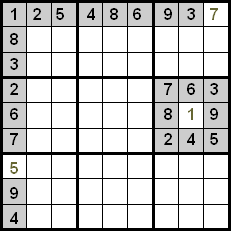
As you can see, all numbers in the first row are placed except 7, so only this number can go in the empty cell. In the first column something similar happens with 5, as well as in the sixth quadrant with 1.

Another way to discover numbers is to make a cross by row and column. This consists of focusing attention on a cell and checking which numbers can go in that position, eliminating those that are in the same row or column.

In the following image we can check that only 7 can go in the indicated cell, because numbers 1, 8, 3, 6 and 9 are in the same column and numbers 2, 4 and 5 in the same row.

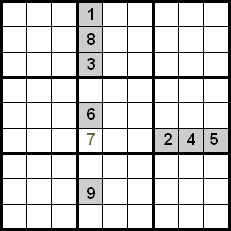
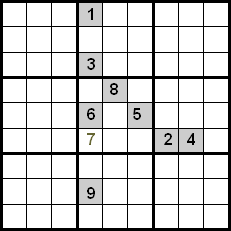
An improvement of this technique is achieved by also controlling the numbers that are in the same quadrant. In the following example we can see that using the cross between rows and columns we would have as candidates numbers 5, 7 and 8 to place them in the marked cell. Since numbers 5 and 8 are already placed in their positions within the quadrant, we can discard them, so number 7 is the one that occupies the indicated position.

The Swordfish technique is used in sudokus when a specific number appears as possible in exactly three rows and three columns.

This method is especially useful for unblocking stuck situations in an advanced game. In a practical case, if you observe that in rows 1, 4 and 7, number 5 can only go in the same three columns, you have identified a Swordfish. Now you can safely remove number 5 from columns 2, 5 and 8 in all other rows, which often clears multiple cells and facilitates the solution of the rest of the sudoku.

XYZ-Wing focuses on finding three cells that form a connection, where two have two possible numbers and the third (pivot) shares a number with each of the other two.

In practice, if you find this configuration in a sudoku game, an opportunity opens up to significantly reduce the possibilities. By applying the XYZ-Wing technique, you can strategically eliminate options, facilitating the resolution of the most complex parts of the puzzle.

The dual linking technique is applied when two numbers can only go in two cells of a row, column or block, and these cells do not contain other numbers.

Imagine a sudoku where in a specific row, only cells A2 and A8 can contain numbers 3 and 7. If we solve that A2 must contain 3, we automatically know that A8 must contain 7.

The box line reduction technique is an advanced strategy that is used when the possible locations of a number in a row or column are entirely within a single region or box.

For example, if in an upper box numbers 4 can only appear in cells that are part of row 2, then you can eliminate 4 as a possibility in the other cells of that box. This technique improves efficiency when solving complex sudokus.