تکنیکیں
سوڈوکو کو حل کرنے کے لیے بہترین تکنیکیں، نکات اور ترکیبیں
پہلے نکات
شروع کرنے کے لیے، آئیے کھیل کے بنیادی اصولوں کا جائزہ لیں:
سوڈوکو ایک 9x9 گرڈ پر مشتمل ہے، جو 9 3x3 کواڈرینٹ میں تقسیم ہے، جسے اس طرح بھرنا ہے کہ تمام قطاروں، کالموں اور کواڈرینٹس میں 1 سے 9 تک کے اعداد بغیر تکرار کے ہوں۔
اس پہلے سبق میں ہم سوڈوکو کو حل کرنے کے لیے کچھ مفید نکات پیش کریں گے۔
- پنسل کا استعمال کریں:کمپیوٹر کی سکرین پر سوڈوکو کرنے سے پنسل میں کرنا زیادہ آرام دہ ہے۔ اس کے علاوہ، پنسل آپ کو اسے آسان طریقے سے مٹانے کی اجازت دیتی ہے۔
- بتدریج مشق کریں:عام طور پر بہت سے اخبارات اور رسالے سوڈوکو کو مشکلات کے لحاظ سے درجہ بندی نہیں کرتے ہیں، لہذا ایک نئے آنے والے کے لیے، ایک پیچیدہ سوڈوکو کو ختم کرنا واقعی مشکل ہو سکتا ہے۔ PrintSudoku.com پر ہم سوڈوکو کو درجہ بندی کرتے ہیں تاکہ آپ اپنی سطح کے مطابق سوڈوکو کے ساتھ مشق کریں۔ سطح جتنی اونچی ہوگی، نمبر ڈالنا اتنا ہی مشکل ہوگا (عام طور پر) اور، بہت مشکل کی صورت میں، بعض اوقات آپ کو چالیں آزمانا ہوں گی۔
- چالیں آزمانے کے لیے، سیل کے اوپری بائیں کونے میں امیدوار نمبر لکھنے سے بہتر کوئی چیز نہیں ہے۔ اگر آپ چھوٹا یا حاشیے میں لکھتے ہیں، جیسے جیسے آپ نمبروں کو مسترد کرتے ہیں، انہیں کاٹتے جائیں۔
- آرام سے لیں:سوڈوکو ایک آرام دہ کھیل ہے۔ کچھ سوڈوکو چند منٹوں میں حل ہو سکتے ہیں لیکن کچھ میں آپ کو گھنٹے یا شاید دن لگ سکتے ہیں۔
- اچھی طرح سے ڈیزائن کیے گئے سوڈوکو کا ایک ہی حل ہوتا ہے، اس خصوصیت کو اپنے فائدے کے لیے استعمال کریں۔
- تمام ممکنہ چالوں کا بغور جائزہ لینے تک کبھی بھی کوشش نہ کریں۔
- ایک ترتیب پر عمل کریں:نمبروں کی جگہ میں، ایک اچھی حکمت عملی یہ ہے کہ سب سے زیادہ کثرت سے آنے والے نمبروں سے شروع کریں اور سب سے کم کثرت سے آنے والے نمبروں پر ختم کریں؛ ٹائی کی صورت میں، ترتیب کا فیصلہ کریں اور پورے کھیل میں اس پر عمل کریں۔
- چیک کریں کہ آپ کا ہر قدم درست ہے، شروع میں ایک غلطی تباہ کن ثابت ہو سکتی ہے۔
- اگر آپ کو کوئی ممکنہ حل نہیں ملتا ہے، تو مدد طلب کریں، یا کسی اور وقت سوڈوکو کی کوشش کریں۔ کئی بار حل اس وقت ظاہر ہوتا ہے جب آپ کو اس کی کم سے کم توقع ہوتی ہے، اور ہمیشہ اس وقت نہیں جب آپ سوڈوکو کے سامنے ہوتے ہیں۔ 😉
بنیادی طریقہ
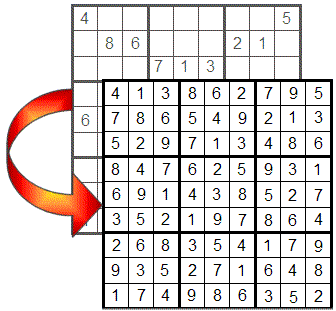
ایک نمبر دریافت کرنے کا سب سے آسان طریقہ یہ ہے کہ جب کسی قطار، کالم یا کواڈرینٹ میں صرف ایک نمبر ڈالنا باقی رہ جائے۔ اس صورت میں، غائب نمبر واحد خالی سیل میں جاتا ہے۔
جیسا کہ آپ دیکھ سکتے ہیں، پہلی قطار میں 7 کے علاوہ تمام نمبر رکھے گئے ہیں، لہذا خالی سیل میں صرف یہی نمبر جا سکتا ہے۔ پہلی کالم میں 5 کے ساتھ بھی ایسا ہی ہوتا ہے، جیسا کہ چھٹے کواڈرینٹ میں 1 کے ساتھ ہوتا ہے۔
قطار اور کالم کے لحاظ سے کراس
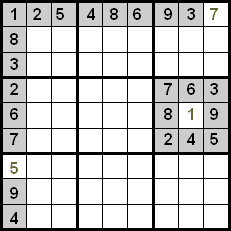
نمبروں کو دریافت کرنے کا ایک اور طریقہ قطار اور کالم کے لحاظ سے کراس کرنا ہے۔ اس میں ایک سیل پر توجہ مرکوز کرنا اور یہ چیک کرنا شامل ہے کہ اس پوزیشن میں کون سے نمبر جا سکتے ہیں، ان کو ختم کرنا جو ایک ہی قطار یا کالم میں ہیں۔
مندرجہ ذیل تصویر میں ہم دیکھ سکتے ہیں کہ اشارہ کردہ سیل میں صرف 7 جا سکتا ہے, کیونکہ نمبر 1, 8, 3, 6 اور 9 ایک ہی کالم میں ہیں اور نمبر 2, 4 اور 5 ایک ہی قطار میں ہیں۔
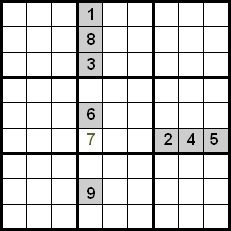
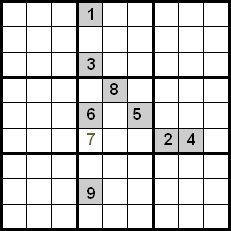
اس تکنیک میں بہتری ایک ہی کواڈرینٹ میں موجود نمبروں کو بھی کنٹرول کرکے حاصل کی جاتی ہے۔ مندرجہ ذیل مثال میں ہم دیکھ سکتے ہیں کہ قطاروں اور کالموں کے درمیان کراس کا استعمال کرتے ہوئے، ہمارے پاس نشان زدہ سیل میں رکھنے کے لیے 5, 7 اور 8 کے امیدوار ہوں گے۔ چونکہ نمبر 5 اور 8 پہلے ہی کواڈرینٹ کے اندر اپنی پوزیشنوں پر رکھے گئے ہیں، ہم انہیں خارج کر سکتے ہیں، لہذا 7 وہ نمبر ہے جو اشارہ کردہ پوزیشن پر قابض ہے۔
سورڈ فش
سورڈ فش (Swordfish) کی تکنیک سوڈوکو میں استعمال ہوتی ہے جب کوئی مخصوص نمبر ٹھیک تین قطاروں اور تین کالموں میں ممکنہ طور پر ظاہر ہوتا ہے۔
💡 عملی مشورہ: مثال کے طور پر، اگر نمبر 5 صرف تین مختلف قطاروں کے 2, 5 اور 8 کالموں میں ظاہر ہو سکتا ہے، تو ایک سورڈ فش پیٹرن بنتا ہے۔ یہاں، اگر 5 ان قطاروں کے 2, 5 اور 8 کالموں سے باہر کسی دوسرے سیل میں نہیں ہو سکتا، تو 5 کو ان کالموں کی دوسری قطاروں میں امکانات کے طور پر ختم کیا جا سکتا ہے۔
یہ طریقہ خاص طور پر ایک اعلی درجے کے کھیل میں پھنسے ہوئے حالات کو کھولنے کے لیے مفید ہے۔ ایک عملی معاملے میں، اگر آپ مشاہدہ کرتے ہیں کہ قطار 1, 4 اور 7 میں، نمبر 5 صرف ایک ہی تین کالموں میں جا سکتا ہے، تو آپ نے ایک سورڈ فش کی شناخت کر لی ہے۔ اب آپ محفوظ طریقے سے نمبر 5 کو تمام دوسری قطاروں کے 2, 5 اور 8 کالموں سے ہٹا سکتے ہیں، جو اکثر متعدد سیلز کو صاف کرتا ہے اور باقی سوڈوکو کو حل کرنے میں سہولت فراہم کرتا ہے۔
XYZ-ونگ
XYZ-ونگ تین سیلز کو تلاش کرنے پر توجہ مرکوز کرتا ہے جو ایک کنکشن بناتے ہیں، جہاں دو میں دو ممکنہ نمبر ہوتے ہیں اور تیسرا (پیوٹ) دوسرے دو میں سے ہر ایک کے ساتھ ایک نمبر شیئر کرتا ہے۔
📝 مثال: فرض کریں کہ تین سیلز ہیں جہاں ایک میں 1 اور 2 کے اختیارات ہیں، دوسرے میں 1 اور 3، اور پیوٹ میں 1, 2, 3 ہیں۔ یہ ترتیب نمبر 1 کو دوسرے سیلز سے ہٹانے کی اجازت دیتی ہے جو تینوں کے ذریعہ دیکھے جاتے ہیں، کیونکہ 1 کو ان میں سے ایک پر قبضہ کرنا ہوگا، اس طرح ان علاقوں میں اختیارات کو واضح کیا جاتا ہے۔
عملی طور پر، اگر آپ کو سوڈوکو کے کھیل میں یہ ترتیب ملتی ہے، تو امکانات کو نمایاں طور پر کم کرنے کا ایک موقع کھل جاتا ہے۔ XYZ-ونگ تکنیک کا اطلاق کرکے، آپ حکمت عملی سے اختیارات کو ختم کر سکتے ہیں، جس سے پہیلی کے زیادہ پیچیدہ حصوں کو حل کرنے میں آسانی ہوتی ہے۔
دوہری لنکنگ
دوہری لنکنگ کی تکنیک اس وقت لاگو ہوتی ہے جب دو نمبر صرف ایک قطار، کالم یا بلاک کے دو سیلز میں جا سکتے ہیں، اور ان سیلز میں دوسرے نمبر نہیں ہوتے ہیں۔
✨ فائدہ: نمبروں میں سے ایک کو حل کرنے سے، دوسرے کی پوزیشن خود بخود حل ہو جاتی ہے۔ یہ تکنیک ان علاقوں میں اختیارات کو ختم کرنے کے لیے موثر ہے جہاں نمبر مضبوطی سے ایک دوسرے سے جڑے ہوئے ہیں۔
ایک سوڈوکو کا تصور کریں جہاں ایک مخصوص قطار میں، صرف سیل A2 اور A8 میں نمبر 3 اور 7 ہو سکتے ہیں۔ اگر ہم حل کرتے ہیں کہ A2 میں 3 ہونا چاہیے، تو ہم خود بخود جانتے ہیں کہ A8 میں 7 ہونا چاہیے۔
باکس لائن میں کمی
باکس لائن میں کمی کی تکنیک ایک اعلی درجے کی حکمت عملی ہے جو اس وقت استعمال ہوتی ہے جب کسی قطار یا کالم میں کسی نمبر کے ممکنہ مقامات مکمل طور پر ایک ہی علاقے یا باکس کے اندر ہوں۔
🔧 اطلاق: اس ترتیب کی شناخت کرنے پر، آپ اس نمبر کو اسی باکس کے دوسرے سیلز میں ممکنہ مقامات سے ہٹا سکتے ہیں جو مخصوص قطار یا کالم میں نہیں ہیں۔
مثال کے طور پر، اگر اوپری باکس میں نمبر 4 صرف قطار 2 کا حصہ بننے والے سیلز میں ظاہر ہو سکتے ہیں، تو آپ اس باکس کے دوسرے سیلز میں 4 کو ایک امکان کے طور پر ہٹا سکتے ہیں۔ یہ تکنیک پیچیدہ سوڈوکو کو حل کرنے میں کارکردگی کو بہتر بناتی ہے۔
کیا آپ مزید تکنیکیں جانتے ہیں؟
اگر آپ سوڈوکو کو حل کرنے کے لیے کوئی اضافی تکنیک جانتے ہیں جس کا ہم نے ذکر نہیں کیا ہے، تو ہم آپ سے سننا پسند کریں گے۔ آپ کا علم دوسرے سوڈوکو کے شوقینوں کو اپنی صلاحیتوں کو بہتر بنانے میں مدد دے سکتا ہے۔