Tehnici
Cele mai bune tehnici, sfaturi și trucuri pentru rezolvarea sudoku-urilor
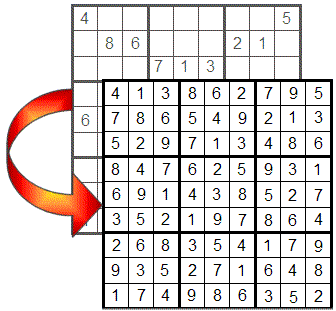
Primele sfaturi
Pentru început, să trecem în revistă regulile de bază ale jocului:
Sudoku constă într-o grilă de 9x9, împărțită în 9 cadrane de 3x3, care trebuie completată astfel încât toate rândurile, coloanele și cadranele să conțină numerele de la 1 la 9 fără repetiție.
În această primă lecție vom prezenta câteva sfaturi utile pentru rezolvarea sudoku-urilor.
- Folosește un creion:Este mult mai confortabil să faci un sudoku cu creionul decât pe ecranul unui computer. În plus, creionul îți permite să ștergi într-un mod simplu.
- Exersează treptat:De obicei, multe ziare și reviste nu clasifică sudoku-urile pe dificultăți, așa că pentru un novice poate fi foarte complicat să termine un sudoku complex. La PrintSudoku.com clasificăm sudoku-urile pentru ca tu să exersezi cu sudoku-uri potrivite nivelului tău. Cu cât nivelul este mai mare, cu atât va fi mai dificil (de obicei) să pui numerele și, în cazul celor foarte dificile, uneori va trebui să încerci mutări.
- Pentru a încerca mutări, nu există nimic mai bun decât să scrii numerele candidate în colțul din stânga sus al celulei. Dacă scrii mic sau pe o margine, pe măsură ce elimini numere, taie-le.
- Ia-o ușor:Sudoku este un joc relaxant. Unele sudoku-uri pot fi rezolvate în câteva minute, dar altele s-ar putea să-ți ia ore sau poate chiar zile.
- Sudoku-urile bine concepute au o singură soluție, folosește această caracteristică în avantajul tău.
- Nu încerca niciodată mutări până nu ai terminat de examinat cu atenție toate mutările posibile.
- Urmează o ordine:În plasarea numerelor, o tactică bună este să începi cu numerele care apar cel mai frecvent, terminând cu cele mai puțin frecvente; în caz de egalitate, decide ordinea și urmeaz-o pe tot parcursul jocului.
- Verifică dacă fiecare pas pe care îl faci este valid, o greșeală la început poate fi dezastruoasă.
- Dacă nu găsești o soluție posibilă, cere ajutor sau încearcă sudoku-ul altă dată. De multe ori soluția apare atunci când te aștepți mai puțin, și nu întotdeauna când ești în fața sudoku-ului. 😉
Metoda de bază
Cel mai simplu mod de a descoperi un număr este atunci când într-un rând, coloană sau cadran a mai rămas un singur număr de pus. În acest caz, numărul lipsă merge în singura căsuță goală.
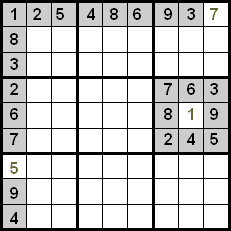
După cum se poate vedea, în primul rând sunt plasate toate numerele, cu excepția lui 7, deci în celula goală poate fi doar acest număr. În prima coloană se întâmplă ceva similar cu 5, la fel ca în al șaselea cadran cu 1.
Încrucișare pe rând și coloană
O altă modalitate de a descoperi numere este prin încrucișarea pe rând și coloană. Aceasta constă în a te concentra pe o căsuță și a verifica ce numere pot fi în acea poziție, eliminându-le pe cele care se află pe același rând sau coloană.
În imaginea următoare putem vedea că în căsuța indicată poate fi doar 7, deoarece numerele 1, 8, 3, 6 și 9 sunt pe aceeași coloană, iar numerele 2, 4 și 5 sunt pe același rând.
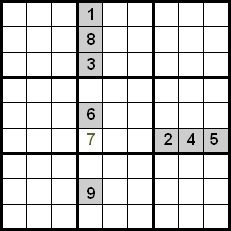
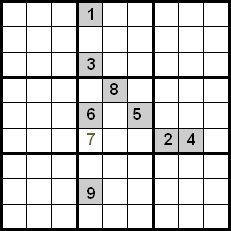
O îmbunătățire a acestei tehnici se obține controlând și numerele care se află în același cadran. În exemplul următor putem vedea că, folosind încrucișarea între rânduri și coloane, am avea ca și candidați numerele 5, 7 și 8 pentru a le plasa în căsuța marcată. Deoarece numerele 5 și 8 sunt deja plasate în pozițiile lor în cadrul cadranului, le putem exclude, deci numărul 7 este cel care ocupă poziția indicată.
Swordfish
Tehnica Swordfish (Peștele-spadă) este utilizată în sudoku atunci când un anumit număr apare ca posibil în exact trei rânduri și trei coloane.
💡 Sfat practic: De exemplu, dacă numărul 5 poate apărea doar în coloanele 2, 5 și 8 din trei rânduri diferite, se formează un model Swordfish. Aici, dacă 5 nu poate fi în nicio altă celulă din acele rânduri în afara coloanelor 2, 5 și 8, atunci 5-urile pot fi eliminate ca posibilități în acele coloane din alte rânduri.
Această metodă este deosebit de utilă pentru a debloca situații blocate într-un joc avansat. Într-un caz practic, dacă observi că în rândurile 1, 4 și 7, numărul 5 poate fi doar în aceleași trei coloane, ai identificat un Swordfish. Acum poți elimina în siguranță numărul 5 din coloanele 2, 5 și 8 din toate celelalte rânduri, ceea ce adesea eliberează mai multe celule și facilitează rezolvarea restului sudoku-ului.
XYZ-Wing
XYZ-Wing se concentrează pe găsirea a trei celule care formează o conexiune, unde două au două numere posibile, iar a treia (pivot) împarte un număr cu fiecare dintre celelalte două.
📝 Exemplu: Să presupunem trei celule unde una are opțiunile 1 și 2, alta 1 și 3, iar pivotul 1, 2, 3. Această configurație permite eliminarea numărului 1 din alte celule care sunt văzute de cele trei, deoarece 1 trebuie să ocupe una dintre ele, clarificând astfel opțiunile în acele zone.
În practică, dacă găsești această configurație într-un joc de sudoku, se deschide o oportunitate de a reduce semnificativ posibilitățile. Aplicând tehnica XYZ-Wing, poți elimina opțiuni în mod strategic, facilitând rezolvarea părților mai complexe ale puzzle-ului.
Legătură dublă (Dual linking)
Tehnica legăturii duble (Dual Linking) se aplică atunci când două numere pot fi doar în două celule dintr-un rând, coloană sau bloc, iar aceste celule nu conțin alte numere.
✨ Avantaj: Rezolvând unul dintre numere, se rezolvă automat poziția celuilalt. Această tehnică este eficientă pentru a elimina opțiuni în zonele în care numerele sunt puternic interconectate.
Imaginează-ți un sudoku în care, într-un anumit rând, doar celulele A2 și A8 pot conține numerele 3 și 7. Dacă rezolvăm că A2 trebuie să conțină 3, știm automat că A8 trebuie să conțină 7.
Reducere linie-cutie (Box line reduction)
Tehnica reducerii linie-cutie (Box Line Reduction) este o strategie avansată care se folosește atunci când posibilele locații ale unui număr într-un rând sau coloană sunt complet în interiorul unei singure regiuni sau cutii.
🔧 Aplicare: Identificând această configurație, poți elimina acel număr din posibilele locații din alte celule ale aceleiași cutii care nu se află în rândul sau coloana specifică.
De exemplu, dacă într-o cutie superioară numerele 4 pot apărea doar în celule care fac parte din rândul 2, atunci poți elimina 4 ca posibilitate în celelalte celule ale acelei cutii. Această tehnică îmbunătățește eficiența la rezolvarea sudoku-urilor complexe.
Cunoști mai multe tehnici?
Dacă cunoști vreo tehnică suplimentară pentru rezolvarea sudoku-urilor pe care nu am menționat-o, ne-ar plăcea să aflăm de la tine. Cunoștințele tale ar putea ajuta alți pasionați de sudoku să-și îmbunătățească abilitățile.