Techniki
Najlepsze techniki, wskazówki i triki do rozwiązywania sudoku
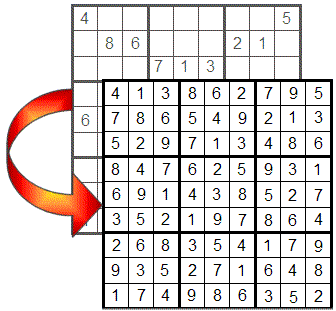
Pierwsze wskazówki
Na początek przeanalizujmy podstawowe zasady gry:
Sudoku składa się z siatki 9x9, podzielonej na 9 kwadrantów 3x3, którą należy wypełnić w taki sposób, aby wszystkie wiersze, kolumny i kwadranty zawierały cyfry od 1 do 9 bez powtórzeń.
W tej pierwszej lekcji przedstawimy kilka przydatnych wskazówek dotyczących rozwiązywania sudoku.
- Użyj ołówka:O wiele wygodniej jest robić sudoku ołówkiem niż na ekranie komputera. Ponadto ołówek pozwala na łatwe wymazanie go.
- Ćwicz stopniowo:Zazwyczaj wiele gazet i czasopism nie klasyfikuje sudoku według trudności, więc dla nowicjusza może być naprawdę skomplikowane ukończenie złożonego sudoku. Na PrintSudoku.com klasyfikujemy sudoku, abyś mógł ćwiczyć z sudoku dopasowanymi do Twojego poziomu. Im wyższy poziom, tym trudniej będzie (zazwyczaj) umieścić liczby, a w przypadku bardzo trudnych, czasami będziesz musiał próbować ruchów.
- Aby spróbować ruchów, nie ma nic lepszego niż pisanie liczb kandydatów w lewym górnym rogu komórki. Jeśli piszesz małe lub na marginesie, w miarę eliminowania liczb, przekreślaj je.
- Spokojnie:Sudoku to relaksująca gra. Niektóre sudoku można rozwiązać w kilka minut, ale inne mogą zająć Ci godziny, a może nawet dni.
- Dobrze zaprojektowane sudoku mają jedno jedyne rozwiązanie, wykorzystaj tę cechę na swoją korzyść.
- Nigdy nie próbuj, dopóki nie skończysz dokładnie badać wszystkich możliwych ruchów.
- Postępuj zgodnie z porządkiem:W umieszczaniu liczb dobrą taktyką jest rozpoczęcie od liczb, które pojawiają się najczęściej, a zakończenie na tych, które pojawiają się najrzadziej; w przypadku remisów zdecyduj o kolejności i postępuj zgodnie z nią przez całą grę.
- Sprawdź, czy każdy Twój krok jest prawidłowy, błąd na początku może być katastrofalny.
- Jeśli nie możesz znaleźć możliwego rozwiązania, poproś o pomoc lub spróbuj sudoku w innym czasie. Wiele razy rozwiązanie pojawia się, gdy najmniej się go spodziewasz, a nie zawsze, gdy jesteś przed sudoku. 😉
Metoda podstawowa
Najłatwiejszym sposobem na odkrycie liczby jest sytuacja, gdy w wierszu, kolumnie lub kwadrancie pozostaje tylko jedna liczba do umieszczenia. W takim przypadku brakująca liczba trafia do jedynej pustej komórki.
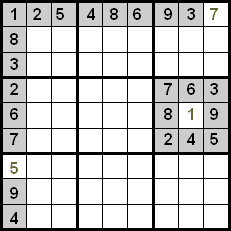
Jak widać, w pierwszym wierszu umieszczono wszystkie liczby oprócz 7, więc w pustej komórce może znajdować się tylko ta liczba. W pierwszej kolumnie dzieje się coś podobnego z 5, podobnie jak w szóstym kwadrancie z 1.
Krzyżowanie wierszy i kolumn
Innym sposobem na odkrycie liczb jest wykonanie krzyżowania wierszy i kolumn. Polega to na skupieniu uwagi na jednej komórce i sprawdzeniu, jakie liczby mogą znajdować się na tej pozycji, eliminując te, które znajdują się w tym samym wierszu lub kolumnie.
Na poniższym obrazku widzimy, że we wskazanej komórce może znajdować się tylko 7, ponieważ liczby 1, 8, 3, 6 i 9 znajdują się w tej samej kolumnie, a liczby 2, 4 i 5 w tym samym wierszu.
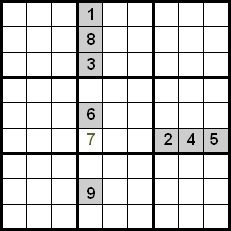
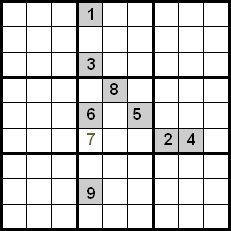
Ulepszenie tej techniki uzyskuje się również poprzez kontrolowanie liczb znajdujących się w tym samym kwadrancie. W poniższym przykładzie widzimy, że używając krzyżowania między wierszami i kolumnami, mielibyśmy kandydatów 5, 7 i 8 do umieszczenia ich w zaznaczonej komórce. Ponieważ liczby 5 i 8 są już umieszczone na swoich pozycjach w kwadrancie, możemy je wykluczyć, dlatego 7 jest liczbą, która zajmuje wskazaną pozycję.
Miecznik
Technika Miecznika (Swordfish) jest używana w sudoku, gdy określona liczba pojawia się jako możliwa w dokładnie trzech wierszach i trzech kolumnach.
💡 Praktyczna wskazówka: Na przykład, jeśli liczba 5 może pojawić się tylko w kolumnach 2, 5 i 8 trzech różnych wierszy, tworzy się wzór Miecznika. Tutaj, jeśli 5 nie może znajdować się w żadnej innej komórce tych wierszy poza kolumnami 2, 5 i 8, to 5 można wyeliminować jako możliwość w tych kolumnach innych wierszy.
Ta metoda jest szczególnie przydatna do odblokowywania zablokowanych sytuacji w zaawansowanej grze. W praktycznym przypadku, jeśli zauważysz, że w wierszach 1, 4 i 7 liczba 5 może iść tylko w tych samych trzech kolumnach, zidentyfikowałeś Miecznika. Teraz możesz bezpiecznie usunąć liczbę 5 z kolumn 2, 5 i 8 we wszystkich innych wierszach, co często czyści wiele komórek i ułatwia rozwiązanie reszty sudoku.
Skrzydło XYZ
Skrzydło XYZ koncentruje się na znalezieniu trzech komórek, które tworzą połączenie, gdzie dwie mają dwie możliwe liczby, a trzecia (oś) dzieli liczbę z każdą z pozostałych dwóch.
📝 Przykład: Załóżmy, że istnieją trzy komórki, w których jedna ma opcje 1 i 2, druga 1 i 3, a oś 1, 2, 3. Ta konfiguracja pozwala na wyeliminowanie liczby 1 z innych komórek, które są widziane przez wszystkie trzy, ponieważ 1 musi zająć jedną z nich, co wyjaśnia opcje w tych obszarach.
W praktyce, jeśli znajdziesz tę konfigurację w grze sudoku, otwiera się możliwość znacznego zmniejszenia możliwości. Stosując technikę Skrzydła XYZ, możesz strategicznie eliminować opcje, ułatwiając rozwiązywanie bardziej złożonych części łamigłówki.
Podwójne łączenie (Dual linking)
Technika podwójnego łączenia (Dual Linking) jest stosowana, gdy dwie liczby mogą iść tylko do dwóch komórek wiersza, kolumny lub bloku, a te komórki nie zawierają innych liczb.
✨ Zaleta: Rozwiązując jedną z liczb, pozycja drugiej jest rozwiązywana automatycznie. Ta technika jest skuteczna w eliminowaniu opcji w obszarach, w których liczby są silnie ze sobą powiązane.
Wyobraź sobie sudoku, w którym w określonym wierszu tylko komórki A2 i A8 mogą zawierać liczby 3 i 7. Jeśli rozwiążemy, że A2 musi zawierać 3, automatycznie wiemy, że A8 musi zawierać 7.
Redukcja linii pudełka (Box line reduction)
Technika redukcji linii pudełka (Box Line Reduction) to zaawansowana strategia stosowana, gdy możliwe lokalizacje liczby w wierszu lub kolumnie znajdują się całkowicie w jednym regionie lub pudełku.
🔧 Zastosowanie: Identyfikując tę konfigurację, możesz wyeliminować tę liczbę z możliwych lokalizacji w innych komórkach tego samego pudełka, które nie znajdują się w określonym wierszu lub kolumnie.
Na przykład, jeśli w górnym pudełku liczby 4 mogą pojawić się tylko w komórkach, które są częścią wiersza 2, możesz wyeliminować 4 jako możliwość w innych komórkach tego pudełka. Ta technika poprawia wydajność podczas rozwiązywania złożonych sudoku.
Znasz więcej technik?
Jeśli znasz jakąś dodatkową technikę rozwiązywania sudoku, której nie wspomnieliśmy, chętnie o niej usłyszymy. Twoja wiedza może pomóc innym fanom sudoku w doskonaleniu swoich umiejętności.