ਤਕਨੀਕਾਂ
ਸੁਡੋਕੁ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਸਭ ਤੋਂ ਵਧੀਆ ਤਕਨੀਕਾਂ, ਸੁਝਾਅ ਅਤੇ ਚਾਲਾਂ
ਪਹਿਲੇ ਸੁਝਾਅ
ਸ਼ੁਰੂ ਕਰਨ ਲਈ, ਆਓ ਖੇਡ ਦੇ ਮੁੱਢਲੇ ਨਿਯਮਾਂ ਦੀ ਸਮੀਖਿਆ ਕਰੀਏ:
ਸੁਡੋਕੁ ਵਿੱਚ ਇੱਕ 9x9 ਗਰਿੱਡ ਹੁੰਦਾ ਹੈ, ਜਿਸਨੂੰ 9 3x3 ਵਰਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ, ਜਿਸਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਭਰਨਾ ਹੁੰਦਾ ਹੈ ਕਿ ਸਾਰੀਆਂ ਕਤਾਰਾਂ, ਕਾਲਮਾਂ ਅਤੇ ਵਰਗਾਂ ਵਿੱਚ 1 ਤੋਂ 9 ਤੱਕ ਦੇ ਅੰਕ ਬਿਨਾਂ ਦੁਹਰਾਓ ਦੇ ਹੋਣ।
ਇਸ ਪਹਿਲੇ ਪਾਠ ਵਿੱਚ, ਅਸੀਂ ਸੁਡੋਕੁ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਕੁਝ ਲਾਭਦਾਇਕ ਸੁਝਾਅ ਪੇਸ਼ ਕਰਾਂਗੇ।
- ਇੱਕ ਪੈਨਸਿਲ ਦੀ ਵਰਤੋਂ ਕਰੋ:ਇੱਕ ਕੰਪਿਊਟਰ ਸਕ੍ਰੀਨ 'ਤੇ ਕਰਨ ਨਾਲੋਂ ਪੈਨਸਿਲ ਨਾਲ ਸੁਡੋਕੁ ਕਰਨਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਆਰਾਮਦਾਇਕ ਹੈ। ਇਸ ਤੋਂ ਇਲਾਵਾ, ਪੈਨਸਿਲ ਤੁਹਾਨੂੰ ਇਸਨੂੰ ਇੱਕ ਸਧਾਰਨ ਤਰੀਕੇ ਨਾਲ ਮਿਟਾਉਣ ਦੀ ਆਗਿਆ ਦਿੰਦੀ ਹੈ।
- ਹੌਲੀ-ਹੌਲੀ ਅਭਿਆਸ ਕਰੋ:ਆਮ ਤੌਰ 'ਤੇ ਬਹੁਤ ਸਾਰੀਆਂ ਅਖਬਾਰਾਂ ਅਤੇ ਰਸਾਲੇ ਸੁਡੋਕੁ ਨੂੰ ਮੁਸ਼ਕਲ ਅਨੁਸਾਰ ਸ਼੍ਰੇਣੀਬੱਧ ਨਹੀਂ ਕਰਦੇ, ਇਸ ਲਈ ਇੱਕ ਨਵੇਂ ਸਿਖਾਂਦਰੂ ਲਈ, ਇੱਕ ਗੁੰਝਲਦਾਰ ਸੁਡੋਕੁ ਨੂੰ ਪੂਰਾ ਕਰਨਾ ਸੱਚਮੁੱਚ ਗੁੰਝਲਦਾਰ ਹੋ ਸਕਦਾ ਹੈ। PrintSudoku.com 'ਤੇ ਅਸੀਂ ਸੁਡੋਕੁ ਨੂੰ ਸ਼੍ਰੇਣੀਬੱਧ ਕਰਦੇ ਹਾਂ ਤਾਂ ਜੋ ਤੁਸੀਂ ਆਪਣੇ ਪੱਧਰ ਦੇ ਅਨੁਸਾਰ ਸੁਡੋਕੁ ਨਾਲ ਅਭਿਆਸ ਕਰ ਸਕੋ। ਪੱਧਰ ਜਿੰਨਾ ਉੱਚਾ ਹੋਵੇਗਾ, ਨੰਬਰ ਲਗਾਉਣਾ ਓਨਾ ਹੀ ਔਖਾ ਹੋਵੇਗਾ (ਆਮ ਤੌਰ 'ਤੇ), ਅਤੇ ਬਹੁਤ ਔਖੇ ਦੇ ਮਾਮਲੇ ਵਿੱਚ, ਕਈ ਵਾਰ ਤੁਹਾਨੂੰ ਚਾਲਾਂ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਨੀ ਪਵੇਗੀ।
- ਚਾਲਾਂ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਨ ਲਈ, ਸੈੱਲ ਦੇ ਉੱਪਰਲੇ ਖੱਬੇ ਕੋਨੇ ਵਿੱਚ ਉਮੀਦਵਾਰ ਨੰਬਰ ਲਿਖਣ ਤੋਂ ਵਧੀਆ ਕੁਝ ਨਹੀਂ ਹੈ। ਜੇਕਰ ਤੁਸੀਂ ਛੋਟਾ ਜਾਂ ਹਾਸ਼ੀਏ 'ਤੇ ਲਿਖਦੇ ਹੋ, ਜਿਵੇਂ ਤੁਸੀਂ ਨੰਬਰਾਂ ਨੂੰ ਖਤਮ ਕਰਦੇ ਹੋ, ਉਹਨਾਂ ਨੂੰ ਕੱਟ ਦਿਓ।
- ਇਸਨੂੰ ਆਰਾਮ ਨਾਲ ਲਓ:ਸੁਡੋਕੁ ਇੱਕ ਆਰਾਮਦਾਇਕ ਖੇਡ ਹੈ। ਕੁਝ ਸੁਡੋਕੁ ਮਿੰਟਾਂ ਵਿੱਚ ਹੱਲ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ ਪਰ ਦੂਜੇ ਤੁਹਾਨੂੰ ਘੰਟੇ ਜਾਂ ਸ਼ਾਇਦ ਦਿਨ ਲੈ ਸਕਦੇ ਹਨ।
- ਚੰਗੀ ਤਰ੍ਹਾਂ ਡਿਜ਼ਾਈਨ ਕੀਤੇ ਸੁਡੋਕੁ ਦਾ ਇੱਕੋ-ਇੱਕ ਹੱਲ ਹੁੰਦਾ ਹੈ, ਇਸ ਵਿਸ਼ੇਸ਼ਤਾ ਨੂੰ ਆਪਣੇ ਫਾਇਦੇ ਲਈ ਵਰਤੋ।
- ਸਾਰੀਆਂ ਸੰਭਾਵੀ ਚਾਲਾਂ ਦੀ ਧਿਆਨ ਨਾਲ ਜਾਂਚ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਕਦੇ ਵੀ ਕੋਸ਼ਿਸ਼ ਨਾ ਕਰੋ।
- ਇੱਕ ਕ੍ਰਮ ਦੀ ਪਾਲਣਾ ਕਰੋ:ਨੰਬਰਾਂ ਦੀ ਪਲੇਸਮੈਂਟ ਵਿੱਚ, ਇੱਕ ਚੰਗੀ ਰਣਨੀਤੀ ਸਭ ਤੋਂ ਵੱਧ ਅਕਸਰ ਆਉਣ ਵਾਲੇ ਨੰਬਰਾਂ ਨਾਲ ਸ਼ੁਰੂ ਕਰਨਾ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਅਕਸਰ ਆਉਣ ਵਾਲੇ ਨੰਬਰਾਂ ਨਾਲ ਖਤਮ ਕਰਨਾ ਹੈ; ਟਾਈ ਹੋਣ ਦੀ ਸਥਿਤੀ ਵਿੱਚ, ਕ੍ਰਮ ਦਾ ਫੈਸਲਾ ਕਰੋ ਅਤੇ ਪੂਰੀ ਖੇਡ ਦੌਰਾਨ ਇਸਦਾ ਪਾਲਣ ਕਰੋ।
- ਜਾਂਚ ਕਰੋ ਕਿ ਤੁਹਾਡਾ ਹਰ ਕਦਮ ਵੈਧ ਹੈ, ਸ਼ੁਰੂ ਵਿੱਚ ਇੱਕ ਗਲਤੀ ਵਿਨਾਸ਼ਕਾਰੀ ਹੋ ਸਕਦੀ ਹੈ।
- ਜੇਕਰ ਤੁਸੀਂ ਕੋਈ ਸੰਭਵ ਹੱਲ ਨਹੀਂ ਲੱਭ ਸਕਦੇ, ਤਾਂ ਮਦਦ ਮੰਗੋ, ਜਾਂ ਕਿਸੇ ਹੋਰ ਸਮੇਂ ਸੁਡੋਕੁ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੋ। ਕਈ ਵਾਰ ਹੱਲ ਉਦੋਂ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ ਜਦੋਂ ਤੁਸੀਂ ਇਸਦੀ ਘੱਟ ਤੋਂ ਘੱਟ ਉਮੀਦ ਕਰਦੇ ਹੋ, ਅਤੇ ਹਮੇਸ਼ਾ ਉਦੋਂ ਨਹੀਂ ਜਦੋਂ ਤੁਸੀਂ ਸੁਡੋਕੁ ਦੇ ਸਾਹਮਣੇ ਹੁੰਦੇ ਹੋ। 😉
ਮੁੱਢਲੀ ਵਿਧੀ
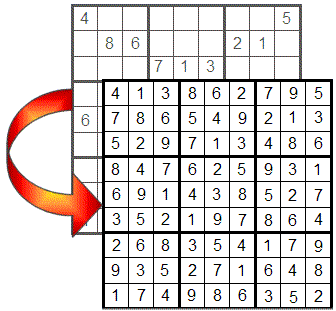
ਇੱਕ ਨੰਬਰ ਨੂੰ ਖੋਜਣ ਦਾ ਸਭ ਤੋਂ ਆਸਾਨ ਤਰੀਕਾ ਹੈ ਜਦੋਂ ਇੱਕ ਕਤਾਰ, ਕਾਲਮ ਜਾਂ ਵਰਗ ਵਿੱਚ ਰੱਖਣ ਲਈ ਸਿਰਫ਼ ਇੱਕ ਨੰਬਰ ਬਚਿਆ ਹੋਵੇ। ਇਸ ਸਥਿਤੀ ਵਿੱਚ, ਗੁੰਮ ਹੋਇਆ ਨੰਬਰ ਇੱਕੋ-ਇੱਕ ਖਾਲੀ ਸੈੱਲ ਵਿੱਚ ਜਾਂਦਾ ਹੈ।
ਜਿਵੇਂ ਕਿ ਤੁਸੀਂ ਦੇਖ ਸਕਦੇ ਹੋ, ਪਹਿਲੀ ਕਤਾਰ ਵਿੱਚ 7 ਨੂੰ ਛੱਡ ਕੇ ਸਾਰੇ ਨੰਬਰ ਰੱਖੇ ਗਏ ਹਨ, ਇਸ ਲਈ ਖਾਲੀ ਸੈੱਲ ਵਿੱਚ ਸਿਰਫ਼ ਇਹੀ ਨੰਬਰ ਹੋ ਸਕਦਾ ਹੈ। ਪਹਿਲੇ ਕਾਲਮ ਵਿੱਚ 5 ਨਾਲ ਵੀ ਅਜਿਹਾ ਹੀ ਹੁੰਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਛੇਵੇਂ ਵਰਗ ਵਿੱਚ 1 ਨਾਲ।
ਕਤਾਰ ਅਤੇ ਕਾਲਮ ਕ੍ਰਾਸਿੰਗ
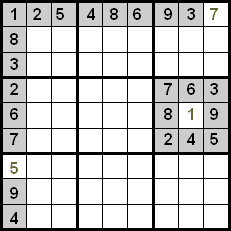
ਨੰਬਰਾਂ ਨੂੰ ਖੋਜਣ ਦਾ ਇੱਕ ਹੋਰ ਤਰੀਕਾ ਹੈ ਕਤਾਰ ਅਤੇ ਕਾਲਮ ਕ੍ਰਾਸਿੰਗ ਕਰਨਾ। ਇਸ ਵਿੱਚ ਇੱਕ ਸੈੱਲ 'ਤੇ ਧਿਆਨ ਕੇਂਦਰਿਤ ਕਰਨਾ ਅਤੇ ਇਹ ਜਾਂਚਣਾ ਸ਼ਾਮਲ ਹੈ ਕਿ ਉਸ ਸਥਿਤੀ ਵਿੱਚ ਕਿਹੜੇ ਨੰਬਰ ਹੋ ਸਕਦੇ ਹਨ, ਉਸੇ ਕਤਾਰ ਜਾਂ ਕਾਲਮ ਵਿੱਚ ਮੌਜੂਦ ਨੰਬਰਾਂ ਨੂੰ ਖਤਮ ਕਰਨਾ।
ਹੇਠਾਂ ਦਿੱਤੀ ਤਸਵੀਰ ਵਿੱਚ ਅਸੀਂ ਦੇਖ ਸਕਦੇ ਹਾਂ ਕਿ ਦਰਸਾਏ ਗਏ ਸੈੱਲ ਵਿੱਚ ਸਿਰਫ਼ 7 ਹੀ ਹੋ ਸਕਦਾ ਹੈ, ਕਿਉਂਕਿ 1, 8, 3, 6 ਅਤੇ 9 ਨੰਬਰ ਇੱਕੋ ਕਾਲਮ ਵਿੱਚ ਹਨ ਅਤੇ 2, 4 ਅਤੇ 5 ਨੰਬਰ ਇੱਕੋ ਕਤਾਰ ਵਿੱਚ ਹਨ।
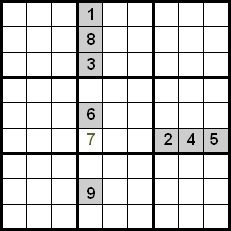
ਇਸ ਤਕਨੀਕ ਵਿੱਚ ਸੁਧਾਰ ਉਸੇ ਵਰਗ ਵਿੱਚ ਮੌਜੂਦ ਨੰਬਰਾਂ ਨੂੰ ਵੀ ਨਿਯੰਤਰਿਤ ਕਰਕੇ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਹੇਠਾਂ ਦਿੱਤੇ ਉਦਾਹਰਣ ਵਿੱਚ ਅਸੀਂ ਦੇਖ ਸਕਦੇ ਹਾਂ ਕਿ ਕਤਾਰਾਂ ਅਤੇ ਕਾਲਮਾਂ ਵਿਚਕਾਰ ਕ੍ਰਾਸਿੰਗ ਦੀ ਵਰਤੋਂ ਕਰਕੇ, ਸਾਡੇ ਕੋਲ 5, 7 ਅਤੇ 8 ਨੰਬਰਾਂ ਦੇ ਉਮੀਦਵਾਰ ਹੋਣਗੇ ਜੋ ਉਹਨਾਂ ਨੂੰ ਚਿੰਨ੍ਹਿਤ ਸੈੱਲ ਵਿੱਚ ਰੱਖਣਗੇ। ਕਿਉਂਕਿ 5 ਅਤੇ 8 ਨੰਬਰ ਪਹਿਲਾਂ ਹੀ ਵਰਗ ਦੇ ਅੰਦਰ ਆਪਣੀਆਂ ਸਥਿਤੀਆਂ 'ਤੇ ਰੱਖੇ ਗਏ ਹਨ, ਅਸੀਂ ਉਹਨਾਂ ਨੂੰ ਬਾਹਰ ਕੱਢ ਸਕਦੇ ਹਾਂ, ਇਸ ਲਈ 7 ਉਹ ਨੰਬਰ ਹੈ ਜੋ ਦਰਸਾਈ ਗਈ ਸਥਿਤੀ 'ਤੇ ਕਬਜ਼ਾ ਕਰਦਾ ਹੈ।
ਸਵੋਰਡਫਿਸ਼
ਸਵੋਰਡਫਿਸ਼ (Swordfish) ਤਕਨੀਕ ਸੁਡੋਕੁ ਵਿੱਚ ਵਰਤੀ ਜਾਂਦੀ ਹੈ ਜਦੋਂ ਇੱਕ ਖਾਸ ਨੰਬਰ ਠੀਕ ਤਿੰਨ ਕਤਾਰਾਂ ਅਤੇ ਤਿੰਨ ਕਾਲਮਾਂ ਵਿੱਚ ਸੰਭਵ ਤੌਰ 'ਤੇ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ।
💡 ਵਿਹਾਰਕ ਸੁਝਾਅ: ਉਦਾਹਰਨ ਲਈ, ਜੇਕਰ 5 ਨੰਬਰ ਸਿਰਫ਼ ਤਿੰਨ ਵੱਖ-ਵੱਖ ਕਤਾਰਾਂ ਦੇ 2, 5 ਅਤੇ 8 ਕਾਲਮਾਂ ਵਿੱਚ ਹੀ ਦਿਖਾਈ ਦੇ ਸਕਦਾ ਹੈ, ਤਾਂ ਇੱਕ ਸਵੋਰਡਫਿਸ਼ ਪੈਟਰਨ ਬਣਦਾ ਹੈ। ਇੱਥੇ, ਜੇਕਰ 5 ਉਹਨਾਂ ਕਤਾਰਾਂ ਦੇ 2, 5 ਅਤੇ 8 ਕਾਲਮਾਂ ਤੋਂ ਬਾਹਰ ਕਿਸੇ ਹੋਰ ਸੈੱਲ ਵਿੱਚ ਨਹੀਂ ਹੋ ਸਕਦਾ, ਤਾਂ 5 ਨੂੰ ਉਹਨਾਂ ਕਾਲਮਾਂ ਦੀਆਂ ਹੋਰ ਕਤਾਰਾਂ ਵਿੱਚ ਸੰਭਾਵਨਾਵਾਂ ਵਜੋਂ ਖਤਮ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।
ਇਹ ਵਿਧੀ ਖਾਸ ਤੌਰ 'ਤੇ ਇੱਕ ਉੱਨਤ ਖੇਡ ਵਿੱਚ ਫਸੇ ਹੋਏ ਹਾਲਾਤਾਂ ਨੂੰ ਅਨਲੌਕ ਕਰਨ ਲਈ ਲਾਭਦਾਇਕ ਹੈ। ਇੱਕ ਵਿਹਾਰਕ ਮਾਮਲੇ ਵਿੱਚ, ਜੇਕਰ ਤੁਸੀਂ ਦੇਖਦੇ ਹੋ ਕਿ 1, 4 ਅਤੇ 7 ਕਤਾਰਾਂ ਵਿੱਚ, 5 ਨੰਬਰ ਸਿਰਫ਼ ਇੱਕੋ ਤਿੰਨ ਕਾਲਮਾਂ ਵਿੱਚ ਹੀ ਜਾ ਸਕਦਾ ਹੈ, ਤਾਂ ਤੁਸੀਂ ਇੱਕ ਸਵੋਰਡਫਿਸ਼ ਦੀ ਪਛਾਣ ਕੀਤੀ ਹੈ। ਹੁਣ ਤੁਸੀਂ ਸੁਰੱਖਿਅਤ ਢੰਗ ਨਾਲ 5 ਨੰਬਰ ਨੂੰ ਹੋਰ ਸਾਰੀਆਂ ਕਤਾਰਾਂ ਦੇ 2, 5 ਅਤੇ 8 ਕਾਲਮਾਂ ਤੋਂ ਹਟਾ ਸਕਦੇ ਹੋ, ਜੋ ਅਕਸਰ ਕਈ ਸੈੱਲਾਂ ਨੂੰ ਸਾਫ਼ ਕਰਦਾ ਹੈ ਅਤੇ ਬਾਕੀ ਸੁਡੋਕੁ ਨੂੰ ਹੱਲ ਕਰਨਾ ਆਸਾਨ ਬਣਾਉਂਦਾ ਹੈ।
XYZ-ਵਿੰਗ
XYZ-ਵਿੰਗ ਤਿੰਨ ਸੈੱਲਾਂ ਨੂੰ ਲੱਭਣ 'ਤੇ ਕੇਂਦ੍ਰਤ ਕਰਦਾ ਹੈ ਜੋ ਇੱਕ ਕੁਨੈਕਸ਼ਨ ਬਣਾਉਂਦੇ ਹਨ, ਜਿੱਥੇ ਦੋ ਵਿੱਚ ਦੋ ਸੰਭਵ ਨੰਬਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਤੀਜਾ (ਪਾਈਵਟ) ਦੂਜੇ ਦੋਵਾਂ ਨਾਲ ਇੱਕ ਨੰਬਰ ਸਾਂਝਾ ਕਰਦਾ ਹੈ।
📝 ਉਦਾਹਰਨ: ਮੰਨ ਲਓ ਕਿ ਤਿੰਨ ਸੈੱਲ ਹਨ ਜਿੱਥੇ ਇੱਕ ਵਿੱਚ 1 ਅਤੇ 2 ਵਿਕਲਪ ਹਨ, ਦੂਜੇ ਵਿੱਚ 1 ਅਤੇ 3, ਅਤੇ ਪਾਈਵਟ ਵਿੱਚ 1, 2, 3 ਹਨ। ਇਹ ਸੰਰਚਨਾ 1 ਨੰਬਰ ਨੂੰ ਤਿੰਨਾਂ ਦੁਆਰਾ ਦੇਖੇ ਗਏ ਹੋਰ ਸੈੱਲਾਂ ਤੋਂ ਹਟਾਉਣ ਦੀ ਆਗਿਆ ਦਿੰਦੀ ਹੈ, ਕਿਉਂਕਿ 1 ਨੂੰ ਉਹਨਾਂ ਵਿੱਚੋਂ ਇੱਕ 'ਤੇ ਕਬਜ਼ਾ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ, ਇਸ ਤਰ੍ਹਾਂ ਉਹਨਾਂ ਖੇਤਰਾਂ ਵਿੱਚ ਵਿਕਲਪਾਂ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰਦਾ ਹੈ।
ਅਭਿਆਸ ਵਿੱਚ, ਜੇਕਰ ਤੁਸੀਂ ਇੱਕ ਸੁਡੋਕੁ ਗੇਮ ਵਿੱਚ ਇਸ ਸੰਰਚਨਾ ਨੂੰ ਲੱਭਦੇ ਹੋ, ਤਾਂ ਸੰਭਾਵਨਾਵਾਂ ਨੂੰ ਕਾਫ਼ੀ ਘੱਟ ਕਰਨ ਦਾ ਇੱਕ ਮੌਕਾ ਖੁੱਲ੍ਹਦਾ ਹੈ। XYZ-ਵਿੰਗ ਤਕਨੀਕ ਨੂੰ ਲਾਗੂ ਕਰਕੇ, ਤੁਸੀਂ ਰਣਨੀਤਕ ਤੌਰ 'ਤੇ ਵਿਕਲਪਾਂ ਨੂੰ ਖਤਮ ਕਰ ਸਕਦੇ ਹੋ, ਜਿਸ ਨਾਲ ਬੁਝਾਰਤ ਦੇ ਵਧੇਰੇ ਗੁੰਝਲਦਾਰ ਹਿੱਸਿਆਂ ਨੂੰ ਹੱਲ ਕਰਨਾ ਆਸਾਨ ਹੋ ਜਾਂਦਾ ਹੈ।
ਦੋਹਰਾ ਲਿੰਕਿੰਗ (Dual linking)
ਦੋਹਰਾ ਲਿੰਕਿੰਗ (Dual Linking) ਤਕਨੀਕ ਉਦੋਂ ਲਾਗੂ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਦੋ ਨੰਬਰ ਸਿਰਫ਼ ਇੱਕ ਕਤਾਰ, ਕਾਲਮ ਜਾਂ ਬਲਾਕ ਦੇ ਦੋ ਸੈੱਲਾਂ ਵਿੱਚ ਹੀ ਜਾ ਸਕਦੇ ਹਨ, ਅਤੇ ਇਹਨਾਂ ਸੈੱਲਾਂ ਵਿੱਚ ਹੋਰ ਨੰਬਰ ਨਹੀਂ ਹੁੰਦੇ।
✨ ਫਾਇਦਾ: ਨੰਬਰਾਂ ਵਿੱਚੋਂ ਇੱਕ ਨੂੰ ਹੱਲ ਕਰਕੇ, ਦੂਜੇ ਦੀ ਸਥਿਤੀ ਆਪਣੇ ਆਪ ਹੱਲ ਹੋ ਜਾਂਦੀ ਹੈ। ਇਹ ਤਕਨੀਕ ਉਹਨਾਂ ਖੇਤਰਾਂ ਵਿੱਚ ਵਿਕਲਪਾਂ ਨੂੰ ਖਤਮ ਕਰਨ ਲਈ ਪ੍ਰਭਾਵਸ਼ਾਲੀ ਹੈ ਜਿੱਥੇ ਨੰਬਰ ਮਜ਼ਬੂਤੀ ਨਾਲ ਆਪਸ ਵਿੱਚ ਜੁੜੇ ਹੋਏ ਹਨ।
ਇੱਕ ਸੁਡੋਕੁ ਦੀ ਕਲਪਨਾ ਕਰੋ ਜਿੱਥੇ ਇੱਕ ਖਾਸ ਕਤਾਰ ਵਿੱਚ, ਸਿਰਫ਼ A2 ਅਤੇ A8 ਸੈੱਲ ਹੀ 3 ਅਤੇ 7 ਨੰਬਰਾਂ ਨੂੰ ਰੱਖ ਸਕਦੇ ਹਨ। ਜੇਕਰ ਅਸੀਂ ਹੱਲ ਕਰਦੇ ਹਾਂ ਕਿ A2 ਵਿੱਚ 3 ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਤਾਂ ਅਸੀਂ ਆਪਣੇ ਆਪ ਜਾਣਦੇ ਹਾਂ ਕਿ A8 ਵਿੱਚ 7 ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ।
ਬਾਕਸ ਲਾਈਨ ਘਟਾਉਣਾ (Box line reduction)
ਬਾਕਸ ਲਾਈਨ ਘਟਾਉਣਾ (Box Line Reduction) ਤਕਨੀਕ ਇੱਕ ਉੱਨਤ ਰਣਨੀਤੀ ਹੈ ਜੋ ਉਦੋਂ ਵਰਤੀ ਜਾਂਦੀ ਹੈ ਜਦੋਂ ਇੱਕ ਕਤਾਰ ਜਾਂ ਕਾਲਮ ਵਿੱਚ ਇੱਕ ਨੰਬਰ ਦੇ ਸੰਭਾਵੀ ਸਥਾਨ ਪੂਰੀ ਤਰ੍ਹਾਂ ਇੱਕ ਖੇਤਰ ਜਾਂ ਬਾਕਸ ਦੇ ਅੰਦਰ ਹੁੰਦੇ ਹਨ।
🔧 ਐਪਲੀਕੇਸ਼ਨ: ਇਸ ਸੰਰਚਨਾ ਦੀ ਪਛਾਣ ਕਰਕੇ, ਤੁਸੀਂ ਉਸ ਨੰਬਰ ਨੂੰ ਉਸੇ ਬਾਕਸ ਦੇ ਹੋਰ ਸੈੱਲਾਂ ਵਿੱਚ ਸੰਭਾਵੀ ਸਥਾਨਾਂ ਤੋਂ ਹਟਾ ਸਕਦੇ ਹੋ ਜੋ ਖਾਸ ਕਤਾਰ ਜਾਂ ਕਾਲਮ ਵਿੱਚ ਨਹੀਂ ਹਨ।
ਉਦਾਹਰਨ ਲਈ, ਜੇਕਰ ਇੱਕ ਉੱਪਰਲੇ ਬਾਕਸ ਵਿੱਚ 4 ਨੰਬਰ ਸਿਰਫ਼ ਕਤਾਰ 2 ਦਾ ਹਿੱਸਾ ਬਣਨ ਵਾਲੇ ਸੈੱਲਾਂ ਵਿੱਚ ਹੀ ਦਿਖਾਈ ਦੇ ਸਕਦੇ ਹਨ, ਤਾਂ ਤੁਸੀਂ ਉਸ ਬਾਕਸ ਦੇ ਹੋਰ ਸੈੱਲਾਂ ਵਿੱਚ 4 ਨੂੰ ਇੱਕ ਸੰਭਾਵਨਾ ਵਜੋਂ ਹਟਾ ਸਕਦੇ ਹੋ। ਇਹ ਤਕਨੀਕ ਗੁੰਝਲਦਾਰ ਸੁਡੋਕੁ ਨੂੰ ਹੱਲ ਕਰਨ ਵੇਲੇ ਕੁਸ਼ਲਤਾ ਵਿੱਚ ਸੁਧਾਰ ਕਰਦੀ ਹੈ।
ਕੀ ਤੁਸੀਂ ਹੋਰ ਤਕਨੀਕਾਂ ਜਾਣਦੇ ਹੋ?
ਜੇਕਰ ਤੁਸੀਂ ਸੁਡੋਕੁ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਕੋਈ ਵਾਧੂ ਤਕਨੀਕ ਜਾਣਦੇ ਹੋ ਜਿਸਦਾ ਅਸੀਂ ਜ਼ਿਕਰ ਨਹੀਂ ਕੀਤਾ ਹੈ, ਤਾਂ ਅਸੀਂ ਤੁਹਾਡੇ ਤੋਂ ਸੁਣਨਾ ਪਸੰਦ ਕਰਾਂਗੇ। ਤੁਹਾਡਾ ਗਿਆਨ ਹੋਰ ਸੁਡੋਕੁ ਪ੍ਰਸ਼ੰਸਕਾਂ ਨੂੰ ਉਹਨਾਂ ਦੇ ਹੁਨਰ ਨੂੰ ਬਿਹਤਰ ਬਣਾਉਣ ਵਿੱਚ ਮਦਦ ਕਰ ਸਕਦਾ ਹੈ।