နည်းစနစ်များ

စတင်ရန်၊ ဂိမ်း၏ အခြေခံစည်းမျဉ်းများကို ပြန်လည်သုံးသပ်ကြပါစို့:

ဤပထမဆုံး သင်ခန်းစာတွင်၊ ကျွန်ုပ်တို့သည် sudoku များကို ဖြေရှင်းရန်အတွက် အသုံးဝင်သော အကြံပြုချက်အချို့ကို တင်ပြပါမည်။

1. ခဲတံသုံးပါ:ကွန်ပျူတာမျက်နှာပြင်ပေါ်တွင်ထက် ခဲတံဖြင့် sudoku လုပ်ခြင်းသည် ပိုမိုသက်တောင့်သက်သာရှိသည်။ ထို့အပြင်၊ ခဲတံသည် သင့်အား ၎င်းကို ရိုးရှင်းသောနည်းလမ်းဖြင့် ဖျက်ရန် ခွင့်ပြုသည်။
2. တဖြည်းဖြည်း လေ့ကျင့်ပါ:များသောအားဖြင့် သတင်းစာများနှင့် မဂ္ဂဇင်းများစွာသည် sudoku များကို အခက်အခဲအလိုက် အမျိုးအစားခွဲခြားခြင်းမရှိပါ၊ ထို့ကြောင့် အသစ်စက်စက်အတွက်၊ ရှုပ်ထွေးသော sudoku တစ်ခုကို ပြီးမြောက်ရန် အမှန်တကယ် ရှုပ်ထွေးနိုင်သည်။ PrintSudoku.com တွင် ကျွန်ုပ်တို့သည် sudoku များကို အမျိုးအစားခွဲခြားသည်၊ သို့မှသာ သင်သည် သင်၏အဆင့်နှင့်ကိုက်ညီသော sudoku များနှင့် လေ့ကျင့်နိုင်မည်ဖြစ်သည်။ အဆင့်မြင့်လေ၊ နံပါတ်များထည့်ရန် ပိုခက်ခဲလေ (များသောအားဖြင့်)၊ နှင့် အလွန်ခက်ခဲသောကိစ္စတွင်၊ တစ်ခါတစ်ရံ သင်သည် လှုပ်ရှားမှုများကို ကြိုးစားရမည်။
3. လှုပ်ရှားမှုများကို ကြိုးစားရန်၊ ဆဲလ်၏ ဘယ်ဘက်အပေါ်ထောင့်တွင် ကိုယ်စားလှယ်လောင်းနံပါတ်များကို ရေးခြင်းထက် ပိုကောင်းသောအရာမရှိပါ။ သင်သေးငယ်သော သို့မဟုတ် အနားသတ်တွင် ရေးပါက၊ သင်နံပါတ်များကို ဖယ်ရှားသည့်အခါ၊ ၎င်းတို့ကို ဖြတ်ပစ်ပါ။
4. ဖြည်းဖြည်းလုပ်ပါ:Sudoku သည် အပန်းဖြေဂိမ်းတစ်ခုဖြစ်သည်။ အချို့ sudoku များကို မိနစ်ပိုင်းအတွင်း ဖြေရှင်းနိုင်သော်လည်း အချို့မှာ သင့်အား နာရီ သို့မဟုတ် ရက်များပင် ကြာနိုင်သည်။
5. ကောင်းမွန်စွာ ဒီဇိုင်းထုတ်ထားသော sudoku များတွင် တစ်ခုတည်းသော အဖြေရှိသည်၊ ဤအင်္ဂါရပ်ကို သင့်အကျိုးအတွက် အသုံးပြုပါ။
6. ဖြစ်နိုင်ခြေရှိသော လှုပ်ရှားမှုအားလုံးကို ဂရုတစိုက် စစ်ဆေးပြီးသည်အထိ ဘယ်တော့မှ မကြိုးစားပါနှင့်။
7. အစီအစဉ်အတိုင်း လိုက်နာပါ:နံပါတ်များထည့်ရာတွင်၊ ကောင်းမွန်သောနည်းဗျူဟာမှာ အများဆုံးပေါ်လာသော နံပါတ်များဖြင့် စတင်ပြီး အနည်းဆုံးပေါ်လာသော နံပါတ်များဖြင့် အဆုံးသတ်ရန်ဖြစ်သည်; သရေကျပါက၊ အစီအစဉ်ကို ဆုံးဖြတ်ပြီး ဂိမ်းတစ်လျှောက်လုံး လိုက်နာပါ။
8. သင်လုပ်ဆောင်သော ခြေလှမ်းတိုင်းသည် မှန်ကန်ကြောင်း စစ်ဆေးပါ၊ အစတွင် အမှားတစ်ခုသည် ဘေးအန္တရာယ်ဖြစ်စေနိုင်သည်။
9. သင်ဖြစ်နိုင်ခြေရှိသော အဖြေကို ရှာမတွေ့ပါက၊ အကူအညီတောင်းပါ၊ သို့မဟုတ် sudoku ကို အခြားအချိန်တွင် ကြိုးစားပါ။ အကြိမ်များစွာ အဖြေသည် သင်အနည်းဆုံးမျှော်လင့်ထားသည့်အခါ ပေါ်လာသည်၊ နှင့် သင် sudoku ရှေ့တွင် ရှိနေသည့်အခါ အမြဲတမ်းမဟုတ်ပါ။ 😉

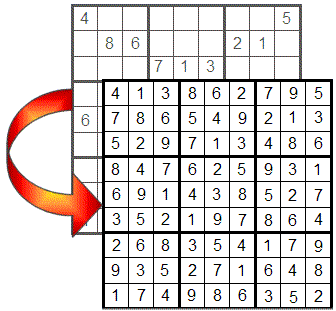
နံပါတ်တစ်ခုကို ရှာဖွေတွေ့ရှိရန် အလွယ်ကူဆုံးနည်းလမ်းမှာ အတန်း၊ ကော်လံ သို့မဟုတ် လေးထောင့်ကွက်တစ်ခုတွင် ထားရန် နံပါတ်တစ်ခုသာ ကျန်ရှိသောအခါဖြစ်သည်။ ဤကိစ္စတွင်၊ ပျောက်ဆုံးနေသော နံပါတ်သည် တစ်ခုတည်းသော လွတ်နေသော ဆဲလ်သို့ သွားသည်။

သင်မြင်သည့်အတိုင်း၊ ပထမအတန်းတွင် ၇ မှလွဲ၍ နံပါတ်အားလုံးကို ထားရှိပြီးဖြစ်သည်၊ ထို့ကြောင့် လွတ်နေသော ဆဲလ်တွင် ဤနံပါတ်သာ ရှိနိုင်သည်။ ပထမကော်လံတွင် ၅ နှင့် အလားတူဖြစ်ပျက်သည်၊ ဆဋ္ဌမလေးထောင့်ကွက်တွင် ၁ နှင့်လည်း အလားတူပင်။

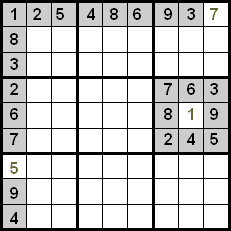
နံပါတ်များကို ရှာဖွေတွေ့ရှိရန် နောက်တစ်နည်းမှာ အတန်းနှင့် ကော်လံ ဖြတ်ကျော်ခြင်း ပြုလုပ်ရန်ဖြစ်သည်။ ၎င်းတွင် ဆဲလ်တစ်ခုပေါ်တွင် အာရုံစိုက်ပြီး ထိုနေရာတွင် မည်သည့်နံပါတ်များ ရှိနိုင်သည်ကို စစ်ဆေးခြင်း၊ တူညီသော အတန်း သို့မဟုတ် ကော်လံတွင် ရှိသော နံပါတ်များကို ဖယ်ရှားခြင်းတို့ ပါဝင်သည်။

အောက်ပါပုံတွင်၊ ညွှန်ပြထားသော ဆဲလ်တွင် ၇ သာ ရှိနိုင်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်၊ အဘယ်ကြောင့်ဆိုသော် ၁၊ ၈၊ ၃၊ ၆ နှင့် ၉ နံပါတ်များသည် တူညီသော ကော်လံတွင် ရှိပြီး ၂၊ ၄ နှင့် ၅ နံပါတ်များသည် တူညီသော အတန်းတွင် ရှိသောကြောင့်ဖြစ်သည်။

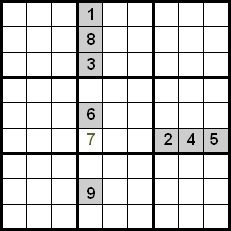
ဤနည်းစနစ်၏ တိုးတက်မှုကို တူညီသော လေးထောင့်ကွက်တွင် ရှိသော နံပါတ်များကိုလည်း ထိန်းချုပ်ခြင်းဖြင့် ရရှိသည်။ အောက်ပါဥပမာတွင်၊ အတန်းများနှင့် ကော်လံများကြား ဖြတ်ကျော်ခြင်းကို အသုံးပြုခြင်းဖြင့်၊ ကျွန်ုပ်တို့တွင် ၅၊ ၇ နှင့် ၈ နံပါတ်များကို အမှတ်အသားပြုထားသော ဆဲလ်တွင် ထားရန် ကိုယ်စားလှယ်လောင်းများ ရှိမည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်။ ၅ နှင့် ၈ နံပါတ်များသည် လေးထောင့်ကွက်အတွင်း ၎င်းတို့၏ နေရာများတွင် ရှိနှင့်ပြီးဖြစ်သောကြောင့်၊ ကျွန်ုပ်တို့သည် ၎င်းတို့ကို ဖယ်ထုတ်နိုင်သည်၊ ထို့ကြောင့် ၇ သည် ညွှန်ပြထားသော နေရာကို သိမ်းပိုက်သည့် နံပါတ်ဖြစ်သည်။

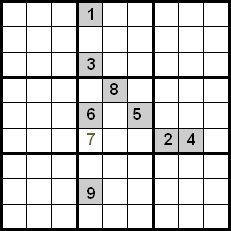
ဓားငါး (Swordfish) နည်းစနစ်ကို sudoku များတွင် အသုံးပြုသည်၊ သီးခြားနံပါတ်တစ်ခုသည် အတိအကျ သုံးတန်းနှင့် သုံးကော်လံတွင် ဖြစ်နိုင်ခြေရှိသည်ဟု ပေါ်လာသောအခါ။

ဤနည်းလမ်းသည် အထူးသဖြင့် အဆင့်မြင့်ဂိမ်းတစ်ခုတွင် ပိတ်မိနေသော အခြေအနေများကို ဖွင့်ရန်အတွက် အသုံးဝင်သည်။ လက်တွေ့ကျသော ကိစ္စတစ်ခုတွင်၊ ၁၊ ၄ နှင့် ၇ အတန်းများတွင်၊ ၅ နံပါတ်သည် တူညီသော သုံးကော်လံများတွင်သာ သွားနိုင်သည်ကို သင်လေ့လာပါက၊ သင်သည် ဓားငါးတစ်ကောင်ကို ဖော်ထုတ်ပြီးဖြစ်သည်။ ယခု သင်သည် ၅ နံပါတ်ကို အခြားအတန်းအားလုံး၏ ၂၊ ၅ နှင့် ၈ ကော်လံများမှ ဘေးကင်းစွာ ဖယ်ရှားနိုင်သည်၊ ၎င်းသည် မကြာခဏ ဆဲလ်များစွာကို ရှင်းလင်းပြီး ကျန်ရှိသော sudoku ၏ အဖြေကို လွယ်ကူစေသည်။

XYZ-တောင်ပံသည် ဆက်သွယ်မှုတစ်ခု ဖန်တီးသည့် ဆဲလ်သုံးခုကို ရှာဖွေခြင်းအပေါ် အာရုံစိုက်သည်၊ ၎င်းတွင် နှစ်ခုတွင် ဖြစ်နိုင်ခြေရှိသော နံပါတ်နှစ်ခုရှိပြီး တတိယ (ပivot) သည် အခြားနှစ်ခုစီနှင့် နံပါတ်တစ်ခုကို မျှဝေသည်။

လက်တွေ့တွင်၊ သင် sudoku ဂိမ်းတစ်ခုတွင် ဤဖွဲ့စည်းပုံကို တွေ့ရှိပါက၊ ဖြစ်နိုင်ခြေများကို သိသိသာသာ လျှော့ချရန် အခွင့်အလမ်းတစ်ခု ဖွင့်လှစ်သည်။ XYZ-တောင်ပံနည်းစနစ်ကို အသုံးချခြင်းဖြင့်၊ သင်သည် ရွေးချယ်စရာများကို မဟာဗျူဟာကျကျ ဖယ်ရှားနိုင်သည်၊ ၎င်းသည် ပဟေဠိ၏ ပိုမိုရှုပ်ထွေးသော အစိတ်အပိုင်းများကို ဖြေရှင်းရန် လွယ်ကူစေသည်။

နှစ်ထပ်ချိတ်ဆက်ခြင်း (Dual Linking) နည်းစနစ်ကို နံပါတ်နှစ်ခုသည် အတန်း၊ ကော်လံ သို့မဟုတ် ဘလောက်တစ်ခု၏ ဆဲလ်နှစ်ခုတွင်သာ သွားနိုင်ပြီး၊ ဤဆဲလ်များတွင် အခြားနံပါတ်များ မပါဝင်သည့်အခါ အသုံးချသည်။

သီးခြားအတန်းတစ်ခုတွင်၊ A2 နှင့် A8 ဆဲလ်များသာ ၃ နှင့် ၇ နံပါတ်များကို ပါဝင်နိုင်သည့် sudoku တစ်ခုကို စိတ်ကူးကြည့်ပါ။ A2 တွင် ၃ ပါဝင်ရမည်ဟု ကျွန်ုပ်တို့ဖြေရှင်းပါက၊ A8 တွင် ၇ ပါဝင်ရမည်ကို ကျွန်ုပ်တို့ အလိုအလျောက် သိရှိသည်။

ဘောက်စ်လိုင်း လျှော့ချခြင်း (Box Line Reduction) နည်းစနစ်သည် အဆင့်မြင့်နည်းဗျူဟာတစ်ခုဖြစ်ပြီး၊ အတန်း သို့မဟုတ် ကော်လံတစ်ခုရှိ နံပါတ်တစ်ခု၏ ဖြစ်နိုင်ခြေရှိသော နေရာများသည် လုံးဝ တစ်ခုတည်းသော ဒေသ သို့မဟုတ် ဘောက်စ်အတွင်းတွင် ရှိနေသည့်အခါ အသုံးပြုသည်။

ဥပမာအားဖြင့်၊ အပေါ်ဘောက်စ်တစ်ခုတွင် ၄ နံပါတ်များသည် အတန်း ၂ ၏ အစိတ်အပိုင်းဖြစ်သော ဆဲလ်များတွင်သာ ပေါ်လာနိုင်ပါက၊ သင်သည် ထိုဘောက်စ်၏ အခြားဆဲလ်များရှိ ဖြစ်နိုင်ခြေတစ်ခုအဖြစ် ၄ ကို ဖယ်ရှားနိုင်သည်။ ဤနည်းစနစ်သည် ရှုပ်ထွေးသော sudoku များကို ဖြေရှင်းသည့်အခါ စွမ်းဆောင်ရည်ကို မြှင့်တင်သည်။