Tehnikas

Lai sāktu, pārskatīsim spēles pamatnoteikumus:

Šajā pirmajā nodarbībā mēs iepazīstināsim ar dažiem noderīgiem padomiem sudoku risināšanai.

1. Izmantojiet zīmuli:Ir daudz ērtāk veikt sudoku ar zīmuli nekā uz datora ekrāna. Turklāt zīmulis ļauj to vienkāršā veidā izdzēst.
2. Vingrinieties pakāpeniski:Parasti daudzi laikraksti un žurnāli neklasificē sudoku pēc grūtības pakāpes, tāpēc iesācējam var būt patiešām sarežģīti pabeigt sarežģītu sudoku. PrintSudoku.com mēs klasificējam sudoku, lai jūs varētu vingrināties ar sudoku, kas atbilst jūsu līmenim. Jo augstāks līmenis, jo grūtāk būs (parasti) ievietot skaitļus, un ļoti grūtu gadījumā dažreiz jums būs jāizmēģina gājieni.
3. Lai izmēģinātu gājienus, nav nekā labāka par kandidātu skaitļu rakstīšanu šūnas augšējā kreisajā stūrī. Ja rakstāt mazu vai malā, kad izslēdzat skaitļus, pārsvītrojiet tos.
4. Ņemiet to mierīgi:Sudoku ir relaksējoša spēle. Dažus sudoku var atrisināt dažu minūšu laikā, bet citi var aizņemt stundas vai varbūt dienas.
5. Labi izstrādātiem sudoku ir viens vienīgs risinājums, izmantojiet šo funkciju savā labā.
6. Nekad nemēģiniet, kamēr neesat rūpīgi izpētījis visus iespējamos gājienus.
7. Ievērojiet secību:Skaitļu izvietošanā laba taktika ir sākt ar skaitļiem, kas parādās visbiežāk, un beigt ar tiem, kas parādās visretāk; neizšķirta gadījumā izlemiet secību un sekojiet tai visā spēlē.
8. Pārbaudiet, vai katrs jūsu solis ir derīgs, kļūda sākumā var būt katastrofāla.
9. Ja nevarat atrast iespējamo risinājumu, lūdziet palīdzību vai izmēģiniet sudoku citā laikā. Daudzas reizes risinājums parādās, kad to vismazāk gaidāt, un ne vienmēr, kad esat sudoku priekšā. 😉

Vieglākais veids, kā atklāt skaitli, ir tad, ja rindā, kolonnā vai kvadrantā ir palicis tikai viens skaitlis, ko ievietot. Šajā gadījumā trūkstošais skaitlis nonāk vienīgajā tukšajā šūnā.

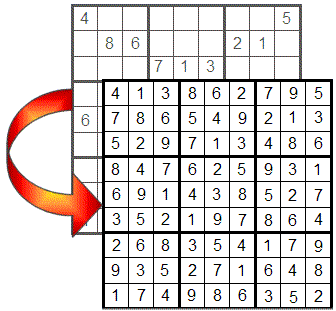
Kā redzat, pirmajā rindā ir ievietoti visi skaitļi, izņemot 7, tāpēc tukšajā šūnā var būt tikai šis skaitlis. Pirmajā kolonnā notiek kaut kas līdzīgs ar 5, tāpat kā sestajā kvadrantā ar 1.

Vēl viens veids, kā atklāt skaitļus, ir veikt rindu un kolonnu krustošanu. Tas sastāv no uzmanības koncentrēšanas uz vienu šūnu un pārbaudes, kuri skaitļi varētu būt šajā pozīcijā, izslēdzot tos, kas atrodas tajā pašā rindā vai kolonnā.

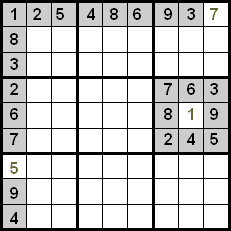
Nākamajā attēlā mēs varam redzēt, ka norādītajā šūnā var būt tikai 7, jo skaitļi 1, 8, 3, 6 un 9 atrodas tajā pašā kolonnā, un skaitļi 2, 4 un 5 atrodas tajā pašā rindā.

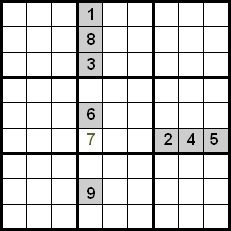
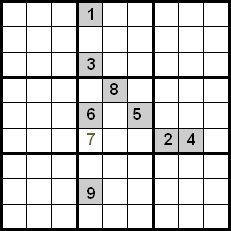
Šīs tehnikas uzlabojums tiek panākts, kontrolējot arī skaitļus, kas atrodas tajā pašā kvadrantā. Nākamajā piemērā mēs varam redzēt, ka, izmantojot krustošanu starp rindām un kolonnām, mums būtu kandidāti 5, 7 un 8, lai tos ievietotu atzīmētajā šūnā. Tā kā skaitļi 5 un 8 jau ir novietoti savās pozīcijās kvadrantā, mēs varam tos izslēgt, tāpēc 7 ir skaitlis, kas ieņem norādīto pozīciju.

Zobenzivs (Swordfish) tehnika tiek izmantota sudoku, kad konkrēts skaitlis parādās kā iespējams tieši trīs rindās un trīs kolonnās.

Šī metode ir īpaši noderīga, lai atbloķētu iestrēgušas situācijas progresīvā spēlē. Praktiskā gadījumā, ja novērojat, ka 1., 4. un 7. rindā skaitlis 5 var iet tikai tajās pašās trīs kolonnās, jūs esat identificējis Zobenzivi. Tagad jūs varat droši noņemt skaitli 5 no 2., 5. un 8. kolonnas visās pārējās rindās, kas bieži vien atbrīvo vairākas šūnas un atvieglo pārējā sudoku risināšanu.

XYZ-spārns koncentrējas uz trīs šūnu atrašanu, kas veido savienojumu, kur divām ir divi iespējamie skaitļi, un trešā (griešanās punkts) dala skaitli ar katru no pārējām divām.

Praksē, ja atrodat šo konfigurāciju sudoku spēlē, paveras iespēja ievērojami samazināt iespējas. Piemērojot XYZ-spārna tehniku, jūs varat stratēģiski izslēgt opcijas, tādējādi atvieglojot sarežģītāko mīklas daļu risināšanu.

Divkāršās saites (Dual Linking) tehnika tiek piemērota, ja divi skaitļi var iet tikai divās rindas, kolonnas vai bloka šūnās, un šīs šūnas nesatur citus skaitļus.

Iedomājieties sudoku, kur noteiktā rindā tikai šūnas A2 un A8 var saturēt skaitļus 3 un 7. Ja mēs atrisinām, ka A2 ir jāsatur 3, mēs automātiski zinām, ka A8 ir jāsatur 7.

Kastes līnijas samazināšanas (Box Line Reduction) tehnika ir progresīva stratēģija, ko izmanto, ja iespējamās skaitļa atrašanās vietas rindā vai kolonnā ir pilnībā viena reģiona vai kastes ietvaros.

Piemēram, ja augšējā kastē skaitļi 4 var parādīties tikai šūnās, kas ir daļa no 2. rindas, tad jūs varat izslēgt 4 kā iespēju citās šīs kastes šūnās. Šī tehnika uzlabo efektivitāti, risinot sarežģītus sudoku.