Technikos
Geriausios technikos, patarimai ir gudrybės sudoku sprendimui
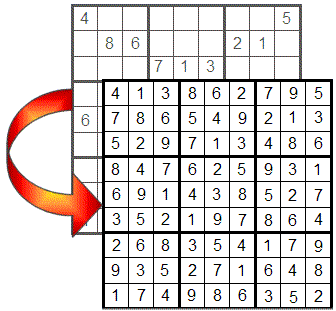
Pirmieji patarimai
Norėdami pradėti, peržiūrėkime pagrindines žaidimo taisykles:
Sudoku susideda iš 9x9 tinklelio, padalinto į 9 3x3 kvadrantus, kurį reikia užpildyti taip, kad visose eilutėse, stulpeliuose ir kvadrantuose būtų skaičiai nuo 1 iki 9 be pasikartojimo.
Šioje pirmoje pamokoje pateiksime keletą naudingų patarimų, kaip spręsti sudoku.
- Naudokite pieštuką:Daug patogiau daryti sudoku pieštuku nei kompiuterio ekrane. Be to, pieštukas leidžia jį paprastu būdu ištrinti.
- Praktikuokitės palaipsniui:Paprastai daugelis laikraščių ir žurnalų neklasifikuoja sudoku pagal sudėtingumą, todėl naujokui gali būti tikrai sudėtinga užbaigti sudėtingą sudoku. PrintSudoku.com mes klasifikuojame sudoku, kad galėtumėte praktikuotis su sudoku, atitinkančiais jūsų lygį. Kuo aukštesnis lygis, tuo sunkiau bus (paprastai) įdėti skaičius, ir labai sunkių atveju kartais teks išbandyti ėjimus.
- Norėdami išbandyti ėjimus, nėra nieko geriau, kaip rašyti kandidatų skaičius ląstelės viršutiniame kairiajame kampe. Jei rašote mažai arba paraštėje, kai pašalinate skaičius, perbraukite juos.
- Ramiai:Sudoku yra atpalaiduojantis žaidimas. Kai kuriuos sudoku galima išspręsti per kelias minutes, bet kiti gali užtrukti valandas ar galbūt dienas.
- Gerai suprojektuoti sudoku turi vieną vienintelį sprendimą, pasinaudokite šia savybe savo naudai.
- Niekada nebandykite, kol neatidžiai išnagrinėjote visų galimų ėjimų.
- Laikykitės tvarkos:Dedant skaičius, gera taktika yra pradėti nuo dažniausiai pasitaikančių skaičių ir baigti rečiausiai pasitaikančiais; lygiųjų atveju nuspręskite tvarką ir laikykitės jos viso žaidimo metu.
- Patikrinkite, ar kiekvienas jūsų žingsnis yra galiojantis, klaida pradžioje gali būti katastrofiška.
- Jei negalite rasti galimo sprendimo, paprašykite pagalbos arba pabandykite sudoku kitu laiku. Daug kartų sprendimas atsiranda, kai mažiausiai to tikitės, ir ne visada, kai esate priešais sudoku. 😉
Pagrindinis metodas
Lengviausias būdas atrasti skaičių yra tada, kai eilutėje, stulpelyje ar kvadrante lieka tik vienas skaičius, kurį reikia įdėti. Tokiu atveju trūkstamas skaičius eina į vienintelę tuščią ląstelę.
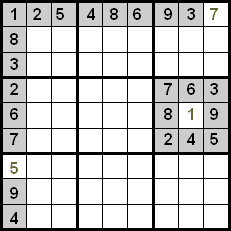
Kaip matote, pirmoje eilutėje yra visi skaičiai, išskyrus 7, todėl tuščioje ląstelėje gali būti tik šis skaičius. Pirmajame stulpelyje kažkas panašaus atsitinka su 5, kaip ir šeštajame kvadrante su 1.
Eilutės ir stulpelio kryžminimas
Kitas būdas atrasti skaičius yra atlikti eilutės ir stulpelio kryžminimą. Tai apima dėmesio sutelkimą į vieną ląstelę ir patikrinimą, kokie skaičiai gali būti toje pozicijoje, pašalinant tuos, kurie yra toje pačioje eilutėje ar stulpelyje.
Kitame paveikslėlyje matome, kad nurodytoje ląstelėje gali būti tik 7, nes skaičiai 1, 8, 3, 6 ir 9 yra tame pačiame stulpelyje, o skaičiai 2, 4 ir 5 yra toje pačioje eilutėje.
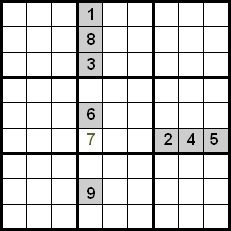
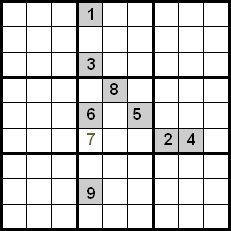
Šios technikos patobulinimas pasiekiamas taip pat kontroliuojant skaičius, esančius tame pačiame kvadrante. Kitame pavyzdyje matome, kad naudojant kryžminimą tarp eilučių ir stulpelių, turėtume kandidatus 5, 7 ir 8, kad juos įdėtume į pažymėtą ląstelę. Kadangi skaičiai 5 ir 8 jau yra savo pozicijose kvadrante, galime juos atmesti, todėl 7 yra skaičius, užimantis nurodytą poziciją.
Kardžuvė
Kardžuvės (Swordfish) technika naudojama sudoku, kai konkretus skaičius pasirodo kaip galimas lygiai trijose eilutėse ir trijuose stulpeliuose.
💡 Praktinis patarimas: Pavyzdžiui, jei skaičius 5 gali pasirodyti tik trijų skirtingų eilučių 2, 5 ir 8 stulpeliuose, susidaro Kardžuvės modelis. Čia, jei 5 negali būti jokioje kitoje tų eilučių ląstelėje už 2, 5 ir 8 stulpelių ribų, tada 5 galima pašalinti kaip galimybę tuose stulpeliuose kitose eilutėse.
Šis metodas ypač naudingas norint atblokuoti įstrigusias situacijas pažengusiame žaidime. Praktiniu atveju, jei pastebite, kad 1, 4 ir 7 eilutėse skaičius 5 gali eiti tik į tuos pačius tris stulpelius, jūs identifikavote Kardžuvę. Dabar galite saugiai pašalinti skaičių 5 iš 2, 5 ir 8 stulpelių visose kitose eilutėse, o tai dažnai išvalo kelias ląsteles ir palengvina likusio sudoku sprendimą.
XYZ sparnas
XYZ sparnas sutelktas į trijų ląstelių, sudarančių ryšį, radimą, kur dvi turi du galimus skaičius, o trečioji (ašis) dalijasi skaičiumi su kiekviena iš kitų dviejų.
📝 Pavyzdys: Tarkime, yra trys ląstelės, kur vienoje yra 1 ir 2 parinktys, kitoje 1 ir 3, o ašyje 1, 2, 3. Ši konfigūracija leidžia pašalinti skaičių 1 iš kitų ląstelių, kurias mato visos trys, nes 1 turi užimti vieną iš jų, taip išaiškinant parinktis tose srityse.
Praktiškai, jei sudoku žaidime rasite šią konfigūraciją, atsiveria galimybė žymiai sumažinti galimybes. Taikydami XYZ sparno techniką, galite strategiškai pašalinti parinktis, palengvindami sudėtingesnių galvosūkio dalių sprendimą.
Dvigubas susiejimas (Dual linking)
Dvigubo susiejimo (Dual Linking) technika taikoma, kai du skaičiai gali eiti tik į dvi eilutės, stulpelio ar bloko ląsteles, o šiose ląstelėse nėra kitų skaičių.
✨ Privalumas: Išsprendus vieną iš skaičių, kito pozicija išsprendžiama automatiškai. Ši technika yra veiksminga norint pašalinti parinktis srityse, kuriose skaičiai yra stipriai susiję.
Įsivaizduokite sudoku, kur tam tikroje eilutėje tik ląstelės A2 ir A8 gali turėti skaičius 3 ir 7. Jei išspręsime, kad A2 turi turėti 3, automatiškai žinome, kad A8 turi turėti 7.
Dėžutės linijos mažinimas (Box line reduction)
Dėžutės linijos mažinimo (Box Line Reduction) technika yra pažangi strategija, naudojama, kai galimos skaičiaus vietos eilutėje ar stulpelyje yra visiškai viename regione ar dėžutėje.
🔧 Taikymas: Identifikavus šią konfigūraciją, galite pašalinti tą skaičių iš galimų vietų kitose tos pačios dėžutės ląstelėse, kurios nėra konkrečioje eilutėje ar stulpelyje.
Pavyzdžiui, jei viršutinėje dėžutėje skaičiai 4 gali pasirodyti tik ląstelėse, kurios yra 2 eilutės dalis, tada galite pašalinti 4 kaip galimybę kitose tos dėžutės ląstelėse. Ši technika pagerina efektyvumą sprendžiant sudėtingus sudoku.
Ar žinote daugiau technikų?
Jei žinote kokią nors papildomą techniką sudoku sprendimui, kurios mes nepaminėjome, norėtume išgirsti iš jūsų. Jūsų žinios gali padėti kitiems sudoku gerbėjams pagerinti savo įgūdžius.