テクニック
数独を解くための最高のテクニック、ヒント、コツ
最初のヒント
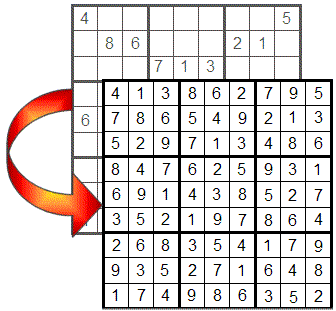
始めるには、ゲームの基本ルールを確認しましょう:
数独は9x9のグリッドで構成され、9つの3x3の象限に分割されており、すべての行、列、象限に1から9までの数字が繰り返しなしで含まれるように埋める必要があります。
この最初のレッスンでは、数独を解くためのいくつかの役立つヒントを紹介します。
- 鉛筆を使用してください:コンピュータの画面よりも鉛筆で数独をする方がはるかに快適です。さらに、鉛筆を使用すると簡単な方法で消すことができます。
- 徐々に練習してください:通常、多くの新聞や雑誌は難易度別に数独を分類していないため、初心者にとっては複雑な数独を完成させるのは本当に複雑な場合があります。PrintSudoku.comでは、あなたのレベルに合った数独で練習できるように数独を分類しています。レベルが高いほど、数字を配置するのが(通常は)難しくなり、非常に難しい場合は、移動を試す必要がある場合があります。
- 移動を試すには、セルの左上隅に候補の数字を書くことほど良いことはありません。小さくまたは余白に書く場合は、数字を消すときに線を引きます。
- 落ち着いてください:数独はリラックスできるゲームです。一部の数独は数分で解決できますが、他の数独は数時間または数日かかる場合があります。
- よく設計された数独には単一の解決策しかありません。この機能を有利に利用してください。
- 考えられるすべての移動を注意深く調べるまで、決して試さないでください。
- 順序に従ってください:数字を配置する際の良い戦術は、最も頻繁に表示される数字から始めて、最も頻繁に表示されない数字で終わることです。引き分けの場合は、順序を決定し、ゲーム全体でそれに従ってください。
- あなたが行うすべてのステップが有効であることを確認してください。最初の間違いは壊滅的なものになる可能性があります。
- 可能な解決策が見つからない場合は、助けを求めるか、別の時間に数独を試してください。多くの場合、解決策は最も期待していないときに表示され、常に数独の前にいるときではありません。😉
基本メソッド
数字を発見する最も簡単な方法は、行、列、または象限に配置する数字が1つだけ残っている場合です。この場合、欠落している数字は唯一の空のセルに入ります。
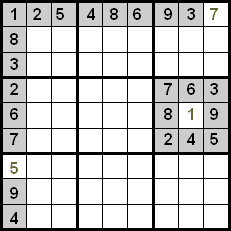
ご覧のとおり、最初の行には7を除くすべての数字が配置されているため、空のセルにはこの数字しかありません。最初の列では5と同様のことが起こり、6番目の象限では1と同様です。
行と列の交差
数字を発見する別の方法は、行と列を交差させることです。これは、1つのセルに注意を集中し、その位置にどの数字があるかを確認し、同じ行または列にあるものを排除することで構成されます。
次の画像では、指定されたセルには7しかないことがわかります。なぜなら、1、8、3、6、9の数字は同じ列にあり、2、4、5の数字は同じ行にあるからです。
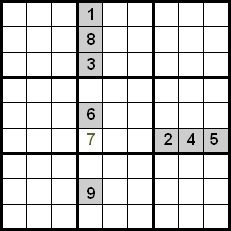
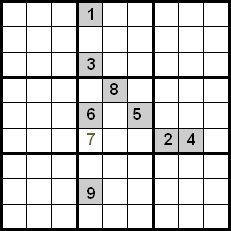
このテクニックの改善は、同じ象限にある数字を制御することによっても達成されます。次の例では、行と列の間の交差を使用して、マークされたセルに配置する候補として5、7、8があることがわかります。5と8の数字はすでに象限内の位置に配置されているため、それらを除外できます。したがって、7が指定された位置を占める数字です。
メカジキ
メカジキ(Swordfish)テクニックは、特定の数字が正確に3つの行と3つの列で可能として表示される場合に数独で使用されます。
💡 実用的なヒント:たとえば、5という数字が3つの異なる行の2、5、8列にしか表示されない場合、メカジキパターンが形成されます。ここで、5がこれらの行の2、5、8列以外の他のセルにない場合、5はこれらの列の他の行の可能性として排除できます。
この方法は、高度なゲームで行き詰まった状況を打開するのに特に役立ちます。実際のケースでは、1、4、7行で5という数字が同じ3つの列にしか行けないことを観察した場合、メカジキを特定したことになります。これで、他のすべての行の2、5、8列から5という数字を安全に削除でき、これにより多くの場合、複数のセルがクリアされ、残りの数独の解決が容易になります。
XYZウィング
XYZウィングは、接続を形成する3つのセルを見つけることに焦点を当てています。ここで、2つは2つの可能な数字を持ち、3つ目(ピボット)は他の2つそれぞれと数字を共有します。
📝 例:1つのセルに1と2のオプションがあり、別のセルに1と3、ピボットに1、2、3がある3つのセルがあるとします。この構成では、1がそれらのいずれかを占有する必要があるため、3つすべてから見える他のセルから1という数字を削除でき、それらの領域のオプションが明確になります。
実際には、数独ゲームでこの構成を見つけた場合、可能性を大幅に減らす機会が開かれます。XYZウィングテクニックを適用することで、戦略的にオプションを排除でき、パズルのより複雑な部分を解決しやすくなります。
デュアルリンク(Dual linking)
デュアルリンク(Dual Linking)テクニックは、2つの数字が行、列、またはブロックの2つのセルにしか行けず、これらのセルに他の数字が含まれていない場合に適用されます。
✨利点:数字の1つを解くと、もう一方の位置が自動的に解決されます。このテクニックは、数字が強く相互接続されている領域でオプションを排除するのに効果的です。
特定の行で、A2とA8のセルにしか3と7の数字を含めることができない数独を想像してみてください。A2に3が含まれている必要があると解決した場合、A8に7が含まれている必要があることを自動的に知ることができます。
ボックスライン削減(Box line reduction)
ボックスライン削減(Box Line Reduction)テクニックは、行または列の数字の可能な場所が完全に単一の領域またはボックス内にある場合に使用される高度な戦略です。
🔧適用:この構成を特定することにより、特定の行または列にない同じボックスの他のセルの可能な場所からその数字を削除できます。
たとえば、上部のボックスで4という数字が2行の一部であるセルにしか表示されない場合、そのボックスの他のセルで4を可能性として削除できます。このテクニックは、複雑な数独を解く際の効率を向上させます。
もっとテクニックを知っていますか?
私たちが言及していない数独を解くための追加のテクニックを知っている場合は、ぜひお聞かせください。あなたの知識は、他の数独ファンがスキルを向上させるのに役立ちます。