Դասեր
Սուդոկու լուծելու լավագույն տեխնիկաները, խորհուրդները և հնարքները
Առաջին խորհուրդներ
Սկսելու համար, եկեք վերանայենք խաղի հիմնական կանոնները.
Սուդոկուն բաղկացած է 9x9 ցանցից, որը բաժանված է 9 3x3 քառորդների, որոնք պետք է լրացվեն այնպես, որ բոլոր տողերը, սյունակները և քառորդները պարունակեն 1-ից 9 թվերը՝ առանց կրկնության։
Այս առաջին դասում մենք կներկայացնենք մի քանի օգտակար խորհուրդներ սուդոկու լուծելու համար։
- Օգտագործեք մատիտ:Շատ ավելի հարմար է սուդոկու անել մատիտով, քան համակարգչի էկրանին։ Բացի այդ, մատիտը թույլ է տալիս հեշտությամբ ջնջել այն։
- Աստիճանաբար մարզվեք:Սովորաբար շատ թերթեր և ամսագրեր չեն դասակարգում սուդոկուները ըստ դժվարության, ուստի նորեկի համար կարող է իսկապես դժվար լինել ավարտել բարդ սուդոկու։ PrintSudoku.com-ում մենք դասակարգում ենք սուդոկուները, որպեսզի դուք կարողանաք մարզվել ձեր մակարդակին համապատասխան սուդոկուներով։ Որքան բարձր է մակարդակը, այնքան դժվար կլինի (սովորաբար) թվերը տեղադրելը, և շատ դժվարների դեպքում երբեմն ստիպված կլինեք գուշակել քայլերը։
- Քայլերը գուշակելու համար ոչինչ ավելի լավ չէ, քան թեկնածու թվերը գրել վանդակի վերին ձախ անկյունում։ Եթե դուք գրում եք փոքր կամ լուսանցքում, ապա թվերը հեռացնելիս դրանք ջնջեք։
- Հանգիստ տարեք:Սուդոկուն հանգստացնող խաղ է։ Որոշ սուդոկուներ կարող են լուծվել մի քանի րոպեում, բայց մյուսները կարող են տևել ժամեր կամ նույնիսկ օրեր։
- Լավ մշակված սուդոկուները ունեն եզակի լուծում, օգտագործեք այս հատկությունը ձեր օգտին։
- Երբեք մի գուշակեք, մինչև մանրակրկիտ չուսումնասիրեք բոլոր հնարավոր քայլերը։
- Հետևեք հերթականությանը:Թվերի տեղադրման ժամանակ լավ մարտավարություն է սկսել ամենից հաճախ հանդիպող թվերից և ավարտել ամենաքիչ հանդիպողներով. ոչ-ոքիի դեպքում որոշեք հերթականությունը և հետևեք դրան ամբողջ խաղի ընթացքում։
- Ստուգեք, որ ձեր կատարած յուրաքանչյուր քայլ վավեր է, սկզբում արված սխալը կարող է աղետալի լինել։
- Եթե չեք կարողանում գտնել հնարավոր լուծում, խնդրեք օգնություն կամ փորձեք սուդոկուն այլ ժամանակ։ Հաճախ լուծումը հայտնվում է, երբ դուք ամենաքիչն եք սպասում, և ոչ միշտ, երբ դուք սուդոկուի առջև եք։ 😉
Հիմնական մեթոդ
Թիվը հայտնաբերելու ամենապարզ եղանակը այն է, երբ տողում, սյունակում կամ քառորդում մնում է միայն մեկ թիվ տեղադրելու համար։ Այս դեպքում բացակայող թիվը գնում է միակ դատարկ վանդակը։
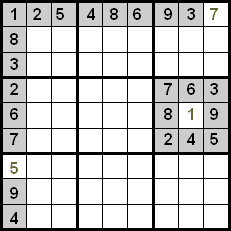
Ինչպես տեսնում եք, առաջին տողում բոլոր թվերը տեղադրված են, բացի 7-ից, ուստի դատարկ վանդակում կարող է լինել միայն այս թիվը։ Առաջին սյունակում նմանատիպ բան է տեղի ունենում 5-ի հետ, ինչպես նաև վեցերորդ քառորդում 1-ի հետ։
Խաչաձևում ըստ տողի և սյունակի
Թվեր հայտնաբերելու մեկ այլ եղանակ է տողի և սյունակի միջոցով խաչաձևում կատարելը։ Սա բաղկացած է ուշադրությունը մեկ վանդակի վրա կենտրոնացնելուց և ստուգելուց, թե որ թվերը կարող են գնալ այդ դիրքում՝ վերացնելով նրանց, ովքեր գտնվում են նույն տողում կամ սյունակում։
Հետևյալ նկարում մենք կարող ենք ստուգել, որ նշված վանդակում կարող է լինել միայն 7-ը, քանի որ 1, 8, 3, 6 և 9 թվերը գտնվում են նույն սյունակում, իսկ 2, 4 և 5 թվերը՝ նույն տողում։
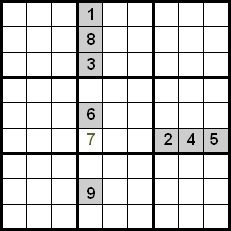
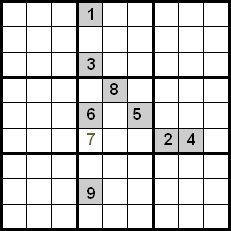
Այս տեխնիկայի բարելավումը ձեռք է բերվում նաև նույն քառորդում գտնվող թվերը վերահսկելով։ Հետևյալ օրինակում մենք կարող ենք տեսնել, որ տողերի և սյունակների միջև խաչաձևումն օգտագործելով՝ մենք կունենայինք 5, 7 և 8 թվերը որպես թեկնածուներ՝ դրանք նշված վանդակում տեղադրելու համար։ Քանի որ 5 և 8 թվերն արդեն տեղադրված են իրենց դիրքերում քառորդի ներսում, մենք կարող ենք դրանք մերժել, ուստի 7 թիվն է, որը զբաղեցնում է նշված դիրքը։
Թրաձուկ
Թրաձուկի տեխնիկան օգտագործվում է սուդոկուներում, երբ որոշակի թիվ հնարավոր է հայտնվում է ճիշտ երեք տողում և երեք սյունակում։
💡 Գործնական խորհուրդ. Օրինակ, եթե 5 թիվը կարող է հայտնվել միայն երեք տարբեր տողերի 2, 5 և 8 սյունակներում, ապա ձևավորվում է Թրաձուկի օրինակ։ Այստեղ, եթե 5-ը չի կարող լինել այդ տողերի որևէ այլ վանդակում՝ բացի 2, 5 և 8 սյունակներից, ապա 5-երը կարող են վերացվել որպես հնարավորություններ այդ սյունակներում՝ այլ տողերից։
Այս մեթոդը հատկապես օգտակար է առաջադեմ խաղում խրված իրավիճակները բացելու համար։ Գործնական դեպքում, եթե դուք նկատում եք, որ 1, 4 և 7 տողերում 5 թիվը կարող է գնալ միայն նույն երեք սյունակներում, դուք հայտնաբերել եք Թրաձուկ։ Այժմ դուք կարող եք ապահով կերպով հեռացնել 5 թիվը 2, 5 և 8 սյունակներից բոլոր մյուս տողերում, ինչը հաճախ մաքրում է բազմաթիվ վանդակներ և հեշտացնում սուդոկուի մնացած մասի լուծումը։
XYZ-թև
XYZ-թևը կենտրոնանում է երեք վանդակների գտնելու վրա, որոնք կապ են ձևավորում, որտեղ երկուսն ունեն երկու հնարավոր թիվ, իսկ երրորդը (առանցքը) կիսում է թիվը մյուս երկուսից յուրաքանչյուրի հետ։
📝 Օրինակ. Ենթադրենք երեք վանդակ, որտեղ մեկն ունի 1 և 2 տարբերակները, մյուսը՝ 1 և 3, իսկ առանցքը՝ 1, 2, 3։ Այս կոնֆիգուրացիան թույլ է տալիս վերացնել 1 թիվը մյուս վանդակներից, որոնք տեսանելի են բոլոր երեքին, քանի որ 1-ը պետք է զբաղեցնի դրանցից մեկը՝ այդպիսով պարզաբանելով տարբերակները այդ տարածքներում։
Գործնականում, եթե դուք գտնում եք այս կոնֆիգուրացիան սուդոկու խաղում, բացվում է հնարավորություն զգալիորեն նվազեցնելու հնարավորությունները։ Կիրառելով XYZ-թևի տեխնիկան՝ դուք կարող եք ռազմավարականորեն վերացնել տարբերակները՝ հեշտացնելով հանելուկի ամենաբարդ մասերի լուծումը։
Երկակի կապ
Երկակի կապի տեխնիկան կիրառվում է, երբ երկու թվեր կարող են գնալ միայն տողի, սյունակի կամ բլոկի երկու վանդակներում, և այդ վանդակները չեն պարունակում այլ թվեր։
✨ Առավելություն. Լուծելով թվերից մեկը՝ դուք ավտոմատ կերպով լուծում եք մյուսի դիրքը։ Այս տեխնիկան արդյունավետ է այն տարածքներում տարբերակները վերացնելու համար, որտեղ թվերը սերտորեն փոխկապակցված են։
Պատկերացրեք սուդոկու, որտեղ որոշակի տողում միայն A2 և A8 վանդակները կարող են պարունակել 3 և 7 թվերը։ Եթե մենք լուծենք, որ A2-ը պետք է պարունակի 3, մենք ավտոմատ կերպով գիտենք, որ A8-ը պետք է պարունակի 7։
Տուփ-գիծ կրճատում
Տուփ-գիծ կրճատման տեխնիկան առաջադեմ ռազմավարություն է, որն օգտագործվում է, երբ թվի հնարավոր դիրքերը տողում կամ սյունակում ամբողջությամբ գտնվում են մեկ տարածաշրջանի կամ տուփի ներսում։
🔧 Կիրառում. Այս կոնֆիգուրացիան բացահայտելով՝ դուք կարող եք վերացնել այդ թիվը նույն տուփի այլ վանդակներում հնարավոր դիրքերից, որոնք չեն գտնվում տվյալ տողում կամ սյունակում։
Օրինակ, եթե վերին տուփում 4 թվերը կարող են հայտնվել միայն այն վանդակներում, որոնք 2-րդ տողի մաս են կազմում, ապա դուք կարող եք վերացնել 4-ը որպես հնարավորություն այդ տուփի մյուս վանդակներում։ Այս տեխնիկան բարելավում է արդյունավետությունը բարդ սուդոկուներ լուծելիս։
Գիտե՞ք ավելի շատ տեխնիկա։
Եթե դուք գիտեք սուդոկու լուծելու որևէ լրացուցիչ տեխնիկա, որը մենք չենք նշել, մենք կցանկանայինք լսել ձեզանից։ Ձեր գիտելիքները կարող են օգնել սուդոկուի այլ երկրպագուներին բարելավել իրենց հմտությունները։