Technikák
A legjobb technikák, tippek és trükkök a sudoku megoldásához
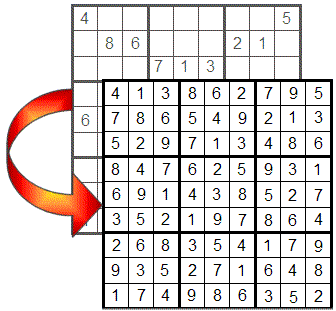
Első tippek
Kezdésként tekintsük át a játék alapvető szabályait:
A Sudoku egy 9x9-es rácsból áll, amely 9 3x3-as kvadránsra van osztva, amelyet úgy kell kitölteni, hogy minden sor, oszlop és kvadráns 1-től 9-ig tartalmazza a számokat ismétlődés nélkül.
Ebben az első leckében bemutatunk néhány hasznos tippet a sudoku megoldásához.
- Használjon ceruzát:Sokkal kényelmesebb ceruzával sudokut csinálni, mint számítógép képernyőjén. Ráadásul a ceruza lehetővé teszi, hogy egyszerűen törölje.
- Gyakoroljon fokozatosan:Általában sok újság és magazin nem osztályozza a sudoku-kat nehézség szerint, így egy neofita számára igazán bonyolult lehet egy komplex sudoku befejezése. A PrintSudoku.com-on osztályozzuk a sudoku-kat, hogy Ön a szintjének megfelelő sudoku-kkal gyakorolhasson. Minél magasabb a szint, annál nehezebb lesz (általában) a számokat elhelyezni, és nagyon nehéz esetben néha meg kell próbálnia a lépéseket.
- A lépések kipróbálásához nincs jobb, mint a jelölt számokat a cella bal felső sarkába írni. Ha kicsiben vagy a margón ír, ahogy kiküszöböli a számokat, húzza át őket.
- Nyugodtan:A sudoku egy pihentető játék. Néhány sudoku percek alatt megoldható, de mások órákig vagy akár napokig is eltarthatnak.
- A jól megtervezett sudoku-knak egyetlen megoldásuk van, használja ezt a funkciót az Ön javára.
- Soha ne próbálkozzon, amíg alaposan meg nem vizsgálta az összes lehetséges lépést.
- Kövesse a sorrendet:A számok elhelyezésénél jó taktika a leggyakrabban megjelenő számokkal kezdeni, és a legritkábban megjelenő számokkal befejezni; döntetlen esetén döntse el a sorrendet, és kövesse azt az egész játék során.
- Ellenőrizze, hogy minden lépése érvényes-e, egy hiba az elején katasztrofális lehet.
- Ha nem talál lehetséges megoldást, kérjen segítséget, vagy próbálja meg a sudokut máskor. Sokszor a megoldás akkor jelenik meg, amikor a legkevésbé számít rá, és nem mindig, amikor a sudoku előtt van. 😉
Alapvető módszer
A szám felfedezésének legegyszerűbb módja, ha egy sorban, oszlopban vagy kvadránsban csak egy számot kell elhelyezni. Ebben az esetben a hiányzó szám az egyetlen üres cellába kerül.
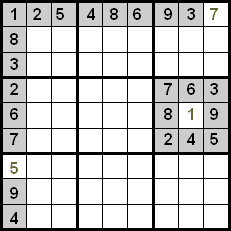
Amint láthatja, az első sorban az összes szám el van helyezve, kivéve a 7-et, tehát az üres cellában csak ez a szám lehet. Az első oszlopban valami hasonló történik az 5-tel, ahogy a hatodik kvadránsban az 1-gyel.
Sor és oszlop keresztezése
A számok felfedezésének másik módja a sor és oszlop keresztezése. Ez abból áll, hogy a figyelmet egy cellára összpontosítjuk, és ellenőrizzük, hogy mely számok lehetnek abban a pozícióban, kiküszöbölve azokat, amelyek ugyanabban a sorban vagy oszlopban vannak.
A következő képen láthatjuk, hogy a megadott cellában csak a 7 lehet, mivel az 1, 8, 3, 6 és 9 számok ugyanabban az oszlopban vannak, a 2, 4 és 5 számok pedig ugyanabban a sorban.
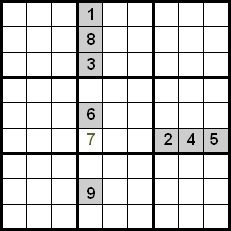
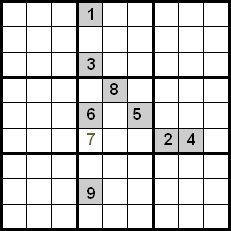
Ennek a technikának a fejlesztése azáltal érhető el, hogy az ugyanabban a kvadránsban lévő számokat is ellenőrizzük. A következő példában láthatjuk, hogy a sorok és oszlopok közötti keresztezést használva a jelölt cellába az 5, 7 és 8 számok lennének a jelöltek. Mivel az 5 és 8 számok már el vannak helyezve a pozíciójukban a kvadránson belül, kizárhatjuk őket, ezért a 7 az a szám, amely a megadott pozíciót foglalja el.
Kardhal
A Kardhal (Swordfish) technikát a sudoku-kban akkor használják, ha egy adott szám pontosan három sorban és három oszlopban lehetségesként jelenik meg.
💡 Gyakorlati tipp: Például, ha az 5-ös szám csak három különböző sor 2., 5. és 8. oszlopában jelenhet meg, akkor Kardhal-minta alakul ki. Itt, ha az 5 nem lehet ezen sorok 2., 5. és 8. oszlopán kívüli más cellában, akkor az 5-öt ki lehet zárni lehetőségként ezen oszlopok más soraiban.
Ez a módszer különösen hasznos a beragadt helyzetek feloldásához egy haladó játékban. Gyakorlati esetben, ha megfigyeli, hogy az 1., 4. és 7. sorban az 5-ös szám csak ugyanabban a három oszlopban mehet, akkor azonosított egy Kardhalat. Most biztonságosan eltávolíthatja az 5-ös számot a 2., 5. és 8. oszlopból az összes többi sorban, ami gyakran több cellát is megtisztít, és megkönnyíti a sudoku többi részének megoldását.
XYZ-szárny
Az XYZ-szárny három olyan cella megtalálására összpontosít, amelyek kapcsolatot alkotnak, ahol kettőnek két lehetséges száma van, a harmadik (forgáspont) pedig megoszt egy számot a másik kettő mindegyikével.
📝 Példa: Tegyük fel, hogy van három cella, ahol az egyiknek 1 és 2 opciója van, a másiknak 1 és 3, a forgáspontnak pedig 1, 2, 3. Ez a konfiguráció lehetővé teszi az 1-es szám eltávolítását más cellákból, amelyeket mindhárom lát, mivel az 1-nek el kell foglalnia az egyiket, ezáltal tisztázva az opciókat ezeken a területeken.
A gyakorlatban, ha megtalálja ezt a konfigurációt egy sudoku játékban, lehetőség nyílik a lehetőségek jelentős csökkentésére. Az XYZ-szárny technikát alkalmazva stratégiailag kiküszöbölheti az opciókat, megkönnyítve a rejtvény bonyolultabb részeinek megoldását.
Kettős összekapcsolás (Dual linking)
A kettős összekapcsolás (Dual Linking) technikát akkor alkalmazzák, ha két szám csak egy sor, oszlop vagy blokk két cellájába mehet, és ezek a cellák nem tartalmaznak más számokat.
✨ Előny: Az egyik szám megoldásával a másik pozíciója automatikusan megoldódik. Ez a technika hatékony az opciók kiküszöbölésére olyan területeken, ahol a számok szorosan összekapcsolódnak.
Képzeljen el egy sudokut, ahol egy adott sorban csak az A2 és A8 cellák tartalmazhatják a 3 és 7 számokat. Ha megoldjuk, hogy az A2-nek 3-at kell tartalmaznia, automatikusan tudjuk, hogy az A8-nak 7-et kell tartalmaznia.
Dobozvonal-csökkentés (Box line reduction)
A dobozvonal-csökkentés (Box Line Reduction) technika egy haladó stratégia, amelyet akkor alkalmaznak, ha egy szám lehetséges helyei egy sorban vagy oszlopban teljesen egyetlen régión vagy dobozon belül vannak.
🔧 Alkalmazás: Ennek a konfigurációnak az azonosításával eltávolíthatja azt a számot a lehetséges helyekről ugyanazon doboz más celláiban, amelyek nem a megadott sorban vagy oszlopban vannak.
Például, ha egy felső dobozban a 4-es számok csak a 2. sor részét képező cellákban jelenhetnek meg, akkor eltávolíthatja a 4-et lehetőségként annak a doboznak a többi cellájában. Ez a technika javítja a hatékonyságot a bonyolult sudoku-k megoldásakor.
Ismer több technikát?
Ha ismer bármilyen további technikát a sudoku megoldásához, amelyet nem említettünk, szívesen hallanánk Öntől. Az Ön tudása segíthet más sudoku-rajongóknak fejleszteni a készségeiket.