तकनीकें
सुडोकू को हल करने के लिए सर्वश्रेष्ठ तकनीकें, सुझाव और तरकीबें
पहले सुझाव
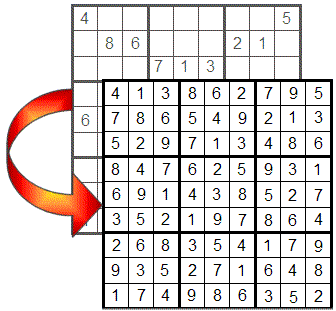
शुरू करने के लिए, आइए खेल के मूल नियमों की समीक्षा करें:
सुडोकू में 9x9 ग्रिड होता है, जिसे 9 3x3 क्वाड्रंट में विभाजित किया गया है, जिसे इस तरह से भरना होता है कि सभी पंक्तियों, स्तंभों और क्वाड्रंट में 1 से 9 तक के अंक बिना पुनरावृत्ति के हों।
इस पहले पाठ में, हम सुडोकू को हल करने के लिए कुछ उपयोगी सुझाव प्रस्तुत करेंगे।
- एक पेंसिल का उपयोग करें:एक कंप्यूटर स्क्रीन पर करने की तुलना में पेंसिल से सुडोकू करना बहुत अधिक आरामदायक है। इसके अलावा, पेंसिल आपको इसे एक सरल तरीके से मिटाने की अनुमति देती है।
- धीरे-धीरे अभ्यास करें:आमतौर पर कई समाचार पत्र और पत्रिकाएँ सुडोकू को कठिनाई के अनुसार वर्गीकृत नहीं करती हैं, इसलिए एक नवजात के लिए, एक जटिल सुडोकू को पूरा करना वास्तव में जटिल हो सकता है। PrintSudoku.com पर हम सुडोकू को वर्गीकृत करते हैं ताकि आप अपने स्तर के अनुसार सुडोकू के साथ अभ्यास कर सकें। स्तर जितना ऊँचा होगा, संख्याएँ रखना उतना ही कठिन होगा (आमतौर पर), और बहुत कठिन के मामले में, कभी-कभी आपको चालें आज़मानी होंगी।
- चालें आज़माने के लिए, सेल के ऊपरी बाएँ कोने में उम्मीदवार संख्याएँ लिखने से बेहतर कुछ नहीं है। यदि आप छोटा या मार्जिन में लिखते हैं, जैसे ही आप संख्याएँ समाप्त करते हैं, उन्हें काट दें।
- इसे आराम से लें:सुडोकू एक आरामदायक खेल है। कुछ सुडोकू मिनटों में हल किए जा सकते हैं लेकिन अन्य आपको घंटे या शायद दिन ले सकते हैं।
- अच्छी तरह से डिज़ाइन किए गए सुडोकू का एक ही समाधान होता है, इस सुविधा का अपने लाभ के लिए उपयोग करें।
- सभी संभावित चालों की सावधानीपूर्वक जाँच करने से पहले कभी भी प्रयास न करें।
- एक क्रम का पालन करें:संख्याओं के स्थान में, एक अच्छी युक्ति सबसे अधिक बार आने वाली संख्याओं से शुरू करना और सबसे कम बार आने वाली संख्याओं के साथ समाप्त करना है; बराबरी के मामले में, क्रम तय करें और पूरे खेल के दौरान उसका पालन करें।
- जाँचें कि आपका हर कदम मान्य है, शुरुआत में एक गलती विनाशकारी हो सकती है।
- यदि आप एक संभावित समाधान नहीं ढूँढ सकते हैं, तो मदद माँगें, या सुडोकू को किसी और समय आज़माएँ। कई बार समाधान तब प्रकट होता है जब आप इसकी कम से कम उम्मीद करते हैं, और हमेशा तब नहीं जब आप सुडोकू के सामने होते हैं। 😉
मूल विधि
एक संख्या को खोजने का सबसे आसान तरीका है जब एक पंक्ति, स्तंभ या क्वाड्रंट में रखने के लिए केवल एक संख्या बची हो। इस मामले में, लापता संख्या एकमात्र खाली सेल में जाती है।
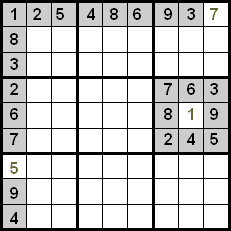
जैसा कि आप देख सकते हैं, पहली पंक्ति में 7 को छोड़कर सभी संख्याएँ रखी गई हैं, इसलिए खाली सेल में केवल यह संख्या हो सकती है। पहले स्तंभ में 5 के साथ ऐसा ही कुछ होता है, छठे क्वाड्रंट में 1 के साथ भी।
पंक्ति और स्तंभ क्रॉसिंग
संख्याओं को खोजने का एक और तरीका है पंक्ति और स्तंभ क्रॉसिंग करना। इसमें एक सेल पर ध्यान केंद्रित करना और उस स्थिति में कौन सी संख्याएँ हो सकती हैं, यह जाँचना, उसी पंक्ति या स्तंभ में मौजूद लोगों को समाप्त करना शामिल है।
निम्नलिखित छवि में हम देख सकते हैं कि इंगित सेल में केवल 7 हो सकता है, क्योंकि 1, 8, 3, 6 और 9 संख्याएँ एक ही स्तंभ में हैं और 2, 4 और 5 संख्याएँ एक ही पंक्ति में हैं।
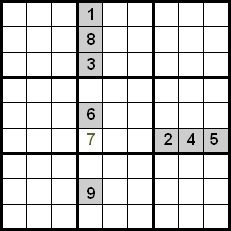
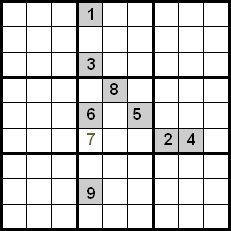
इस तकनीक में सुधार उसी क्वाड्रंट में मौजूद संख्याओं को भी नियंत्रित करके प्राप्त किया जाता है। निम्नलिखित उदाहरण में हम देख सकते हैं कि पंक्तियों और स्तंभों के बीच क्रॉसिंग का उपयोग करके, हमारे पास 5, 7 और 8 संख्याएँ उम्मीदवार के रूप में होंगी जिन्हें चिह्नित सेल में रखा जाएगा। चूँकि 5 और 8 संख्याएँ पहले से ही क्वाड्रंट के भीतर अपनी स्थिति में रखी गई हैं, हम उन्हें बाहर कर सकते हैं, इसलिए 7 वह संख्या है जो इंगित स्थिति पर कब्जा करती है।
स्वोर्डफ़िश
स्वोर्डफ़िश (Swordfish) तकनीक सुडोकू में उपयोग की जाती है, जब एक विशिष्ट संख्या ठीक तीन पंक्तियों और तीन स्तंभों में संभव के रूप में दिखाई देती है।
💡 व्यावहारिक सुझाव: उदाहरण के लिए, यदि 5 संख्या तीन अलग-अलग पंक्तियों के 2, 5 और 8 स्तंभों में ही दिखाई दे सकती है, तो एक स्वोर्डफ़िश पैटर्न बनता है। यहाँ, यदि 5 उन पंक्तियों के 2, 5 और 8 स्तंभों के बाहर किसी अन्य सेल में नहीं हो सकता है, तो 5 को उन स्तंभों की अन्य पंक्तियों में संभावनाओं के रूप में समाप्त किया जा सकता है।
यह विधि विशेष रूप से एक उन्नत खेल में फंसी हुई स्थितियों को अनलॉक करने के लिए उपयोगी है। एक व्यावहारिक मामले में, यदि आप देखते हैं कि 1, 4 और 7 पंक्तियों में, 5 संख्या एक ही तीन स्तंभों में ही जा सकती है, तो आपने एक स्वोर्डफ़िश की पहचान की है। अब आप सुरक्षित रूप से 5 संख्या को अन्य सभी पंक्तियों के 2, 5 और 8 स्तंभों से हटा सकते हैं, जो अक्सर कई सेलों को साफ़ करता है और शेष सुडोकू के समाधान को सुगम बनाता है।
XYZ-विंग
XYZ-विंग एक कनेक्शन बनाने वाले तीन सेलों को खोजने पर ध्यान केंद्रित करता है, जहाँ दो में दो संभावित संख्याएँ होती हैं और तीसरा (पिवट) अन्य दो में से प्रत्येक के साथ एक संख्या साझा करता है।
📝 उदाहरण: मान लीजिए कि तीन सेल हैं जहाँ एक में 1 और 2 विकल्प हैं, दूसरे में 1 और 3, और पिवट में 1, 2, 3 हैं। यह कॉन्फ़िगरेशन 1 संख्या को तीनों द्वारा देखे गए अन्य सेलों से समाप्त करने की अनुमति देता है, क्योंकि 1 उनमें से एक पर कब्जा करना चाहिए, इस प्रकार उन क्षेत्रों में विकल्पों को स्पष्ट करता है।
व्यवहार में, यदि आप एक सुडोकू गेम में यह कॉन्फ़िगरेशन पाते हैं, तो संभावनाओं को काफी कम करने का एक अवसर खुलता है। XYZ-विंग तकनीक को लागू करके, आप रणनीतिक रूप से विकल्पों को समाप्त कर सकते हैं, जिससे पहेली के अधिक जटिल भागों को हल करना आसान हो जाता है।
दोहरी लिंकिंग (Dual linking)
दोहरी लिंकिंग (Dual Linking) तकनीक तब लागू होती है जब दो संख्याएँ केवल एक पंक्ति, स्तंभ या ब्लॉक के दो सेलों में ही जा सकती हैं, और इन सेलों में अन्य संख्याएँ नहीं होती हैं।
✨ लाभ: संख्याओं में से एक को हल करके, दूसरे की स्थिति स्वचालित रूप से हल हो जाती है। यह तकनीक उन क्षेत्रों में विकल्पों को समाप्त करने के लिए प्रभावी है जहाँ संख्याएँ दृढ़ता से परस्पर जुड़ी हुई हैं।
एक सुडोकू की कल्पना करें जहाँ एक विशिष्ट पंक्ति में, केवल A2 और A8 सेल ही 3 और 7 संख्याएँ रख सकते हैं। यदि हम हल करते हैं कि A2 में 3 होना चाहिए, तो हम स्वचालित रूप से जानते हैं कि A8 में 7 होना चाहिए।
बॉक्स लाइन कटौती (Box line reduction)
बॉक्स लाइन कटौती (Box Line Reduction) तकनीक एक उन्नत रणनीति है जो तब उपयोग की जाती है जब एक पंक्ति या स्तंभ में एक संख्या के संभावित स्थान पूरी तरह से एक ही क्षेत्र या बॉक्स के भीतर होते हैं।
🔧 अनुप्रयोग: इस कॉन्फ़िगरेशन की पहचान करके, आप उस संख्या को उसी बॉक्स के अन्य सेलों में संभावित स्थानों से समाप्त कर सकते हैं जो विशिष्ट पंक्ति या स्तंभ में नहीं हैं।
उदाहरण के लिए, यदि एक ऊपरी बॉक्स में 4 संख्याएँ केवल पंक्ति 2 का हिस्सा बनने वाले सेलों में ही दिखाई दे सकती हैं, तो आप उस बॉक्स के अन्य सेलों में 4 को एक संभावना के रूप में समाप्त कर सकते हैं। यह तकनीक जटिल सुडोकू को हल करते समय दक्षता में सुधार करती है।
क्या आप और तकनीकें जानते हैं?
यदि आप सुडोकू को हल करने के लिए कोई अतिरिक्त तकनीक जानते हैं जिसका हमने उल्लेख नहीं किया है, तो हम आपसे सुनना पसंद करेंगे। आपका ज्ञान अन्य सुडोकू प्रशंसकों को उनके कौशल को बेहतर बनाने में मदद कर सकता है।