Lecionoj
La plej bonaj teknikoj, konsiloj kaj trukoj por solvi sudokojn
Unuaj konsiloj
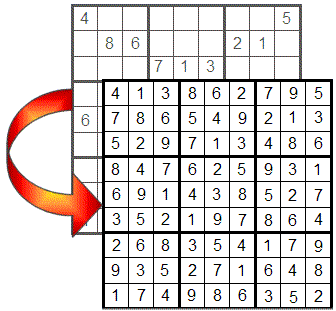
Por komenci, ni reviziu la bazajn regulojn de la ludo:
Sudoku konsistas el 9x9 krado, dividita en 9 3x3 kvadrantojn, kiujn oni devas plenigi tiel, ke ĉiuj vicoj, kolumnoj kaj kvadrantoj enhavu la nombrojn de 1 ĝis 9 sen ripeto.
En ĉi tiu unua leciono ni prezentos kelkajn utilajn konsilojn por solvi sudokojn.
- Uzu krajonon:Estas multe pli komforte fari sudokun per krajono ol sur komputila ekrano. Krome, la krajono permesas vin facile forviŝi ĝin.
- Praktiku iom post iom:Kutime multaj gazetoj kaj revuoj ne klasifikas sudokojn laŭ malfacileco, do por novulo, povas esti vere malfacile fini kompleksan sudokun. Ĉe PrintSudoku.com ni klasifikas la sudokojn por ke vi povu praktiki kun sudokoj laŭ via nivelo. Ju pli alta estas la nivelo, des pli malfacile (kutime) estos meti la nombrojn kaj, en la kazo de tre malfacilaj, foje vi devos diveni movojn.
- Por diveni movojn, ne ekzistas pli bona ol skribi la kandidatajn nombrojn en la supra maldekstra angulo de la ĉelo. Se vi skribas malgrandan aŭ en marĝeno, dum vi forĵetas nombrojn, forstreku ilin.
- Trankviliĝu:Sudoku estas malstreĉa ludo. Kelkaj sudokoj povas esti solvitaj en kelkaj minutoj, sed aliaj eble daŭros horojn aŭ eble tagojn.
- Bone desegnitaj sudokoj havas unikan solvon, uzu ĉi tiun karakterizaĵon al via avantaĝo.
- Neniam divenu antaŭ ol vi zorge ekzamenis ĉiujn eblajn movojn.
- Sekvu ordon:En la lokigo de la nombroj, bona taktiko estas komenci per la nombroj, kiuj aperas plej ofte, finante per la malpli oftaj; en kazo de egaleco, decidu la ordon kaj sekvu ĝin dum la tuta ludo.
- Kontrolu, ke ĉiu paŝo, kiun vi faras, estas valida, eraro komence povas esti katastrofa.
- Se vi ne trovas eblan solvon, petu helpon, aŭ provu la sudokun alian fojon. Ofte la solvo aperas kiam vi malplej atendas ĝin, kaj ne ĉiam kiam vi estas antaŭ la sudoku. 😉
Baza metodo
La plej simpla maniero malkovri nombron estas kiam en vico, kolumno aŭ kvadranto restas nur unu nombro por meti. En ĉi tiu kazo la mankanta nombro iras en la sola malplena ĉelo.
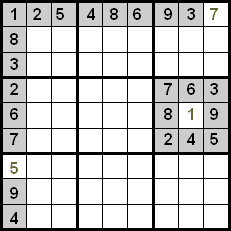
Kiel videblas, en la unua vico estas ĉiuj nombroj krom 7, do en la malplena ĉelo povas iri nur ĉi tiu nombro. En la unua kolumno okazas io simila kun 5, same kiel en la sesa kvadranto kun 1.
Kruco laŭ vico kaj kolumno
Alia maniero malkovri nombrojn estas fari krucon laŭ vico kaj kolumno. Ĉi tio konsistas el koncentri la atenton al ĉelo kaj kontroli, kiuj nombroj povas iri en tiun pozicion, eliminante tiujn, kiuj estas en la sama vico aŭ kolumno.
En la sekva bildo ni povas kontroli, ke en la indikita ĉelo povas iri nur 7, ĉar la nombroj 1, 8, 3, 6 kaj 9 estas en la sama kolumno kaj la nombroj 2, 4 kaj 5 en la sama vico.
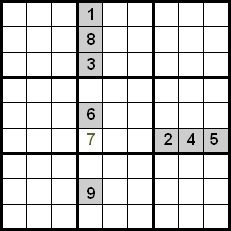
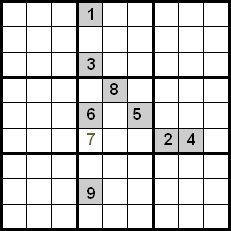
Plibonigo de ĉi tiu tekniko estas atingita ankaŭ kontrolante la nombrojn, kiuj estas en la sama kvadranto. En la sekva ekzemplo ni povas vidi, ke uzante la krucon inter vicoj kaj kolumnoj ni havus kiel kandidatojn la nombrojn 5, 7 kaj 8 por meti ilin en la markitan ĉelon. Ĉar la nombroj 5 kaj 8 jam estas metitaj en siaj pozicioj ene de la kvadranto, ni povas forĵeti ilin, do la nombro 7 estas tiu, kiu okupas la indikitan pozicion.
Glavfiŝo
La tekniko de la Glavfiŝo estas uzata en sudokoj kiam specifa nombro aperas kiel ebla en ekzakte tri vicoj kaj tri kolumnoj.
💡 Praktika Konsilo: Ekzemple, se la nombro 5 povas aperi nur en la kolumnoj 2, 5 kaj 8 de tri malsamaj vicoj, formiĝas Glavfiŝo-modelo. Ĉi tie, se 5 ne povas esti en iu ajn alia ĉelo de tiuj vicoj ekster la kolumnoj 2, 5 kaj 8, tiam la 5-oj povas esti forigitaj kiel eblecoj en tiuj kolumnoj de aliaj vicoj.
Ĉi tiu metodo estas precipe utila por malbloki blokitajn situaciojn en altnivela ludo. En praktika kazo, se vi observas, ke en la vicoj 1, 4 kaj 7, la nombro 5 povas iri nur en la samaj tri kolumnoj, vi identigis Glavfiŝon. Nun vi povas sekure forigi la nombron 5 el la kolumnoj 2, 5 kaj 8 en ĉiuj aliaj vicoj, kio ofte malplenigas plurajn ĉelojn kaj faciligas la solvon de la resto de la sudoku.
XYZ-flugilo
XYZ-flugilo fokusiĝas al la trovo de tri ĉeloj, kiuj formas konekton, kie du havas du eblajn nombrojn kaj la tria (pivoto) dividas nombron kun ĉiu el la aliaj du.
📝 Ekzemplo: Supozu tri ĉelojn, kie unu havas la opciojn 1 kaj 2, alia 1 kaj 3, kaj la pivoto 1, 2, 3. Ĉi tiu agordo permesas forigi la nombron 1 el aliaj ĉeloj, kiuj estas viditaj de la tri, ĉar la 1 devas okupi unu el ili, tiel klarigante la opciojn en tiuj areoj.
En la praktiko, se vi trovas ĉi tiun agordon en sudoku-ludo, malfermiĝas okazo por signife redukti la eblecojn. Aplikante la teknikon XYZ-flugilo, vi povas forigi opciojn strategie, faciligante la solvon de la plej kompleksaj partoj de la enigmo.
Duobla ligilo
La tekniko de duobla ligilo estas aplikata kiam du nombroj povas iri nur en du ĉelojn de vico, kolumno aŭ bloko, kaj ĉi tiuj ĉeloj ne enhavas aliajn nombrojn.
✨ Avantaĝo: Solvante unu el la nombroj, vi aŭtomate solvas la pozicion de la alia. Ĉi tiu tekniko estas efika por forigi opciojn en areoj kie la nombroj estas forte interkonektitaj.
Imagu sudokun kie en specifa vico, nur la ĉeloj A2 kaj A8 povas enhavi la nombrojn 3 kaj 7. Se ni solvas, ke A2 devas enhavi 3, ni aŭtomate scias, ke A8 devas enhavi 7.
Kesto-linio-redukto
La tekniko de kesto-linio-redukto estas altnivela strategio, kiu estas uzata kiam la eblaj lokoj de nombro en vico aŭ kolumno estas tute ene de ununura regiono aŭ kesto.
🔧 Apliko: Identigante ĉi tiun agordon, vi povas forigi tiun nombron el la eblaj lokoj en aliaj ĉeloj de la sama kesto, kiuj ne estas en la specifa vico aŭ kolumno.
Ekzemple, se en supra kesto la nombroj 4 povas aperi nur en ĉeloj, kiuj estas parto de vico 2, tiam vi povas forigi 4 kiel eblecon en la aliaj ĉeloj de tiu kesto. Ĉi tiu tekniko plibonigas la efikecon dum solvado de kompleksaj sudokoj.
Ĉu vi konas pli da teknikoj?
Se vi konas iun aldonan teknikon por solvi sudokojn, kiun ni ne menciis, ni ŝatus aŭdi de vi. Via scio povus helpi aliajn sudoku-ŝatantojn plibonigi siajn kapablojn.