Μαθήματα

Για να ξεκινήσουμε, ας αναθεωρήσουμε τους βασικούς κανόνες του παιχνιδιού:

Σε αυτό το πρώτο μάθημα θα παρουσιάσουμε μερικές χρήσιμες συμβουλές για την επίλυση σουντόκου.

1. Χρησιμοποιήστε μολύβι:Είναι πολύ πιο άνετο να κάνετε ένα σουντόκου με μολύβι παρά σε οθόνη υπολογιστή. Επιπλέον, το μολύβι σας επιτρέπει να το σβήσετε εύκολα.
2. Εξασκηθείτε σταδιακά:Συνήθως πολλές εφημερίδες και περιοδικά δεν κατηγοριοποιούν τα σουντόκου ανάλογα με τη δυσκολία, οπότε για έναν αρχάριο, μπορεί να είναι πολύ δύσκολο να ολοκληρώσει ένα σύνθετο σουντόκου. Στο PrintSudoku.com κατηγοριοποιούμε τα σουντόκου έτσι ώστε να μπορείτε να εξασκηθείτε με σουντόκου ανάλογα με το επίπεδό σας. Όσο υψηλότερο είναι το επίπεδο, τόσο πιο δύσκολο (συνήθως) θα είναι να τοποθετήσετε τους αριθμούς και, στην περίπτωση των πολύ δύσκολων, μερικές φορές θα πρέπει να μαντέψετε κινήσεις.
3. Για να μαντέψετε κινήσεις, δεν υπάρχει τίποτα καλύτερο από το να γράψετε τους υποψήφιους αριθμούς στην επάνω αριστερή γωνία του κελιού. Εάν γράφετε μικρά ή στο περιθώριο, καθώς απορρίπτετε αριθμούς, διαγράψτε τους.
4. Πάρτε το χαλαρά:Το σουντόκου είναι ένα χαλαρωτικό παιχνίδι. Ορισμένα σουντόκου μπορούν να λυθούν σε λίγα λεπτά, αλλά άλλα μπορεί να σας πάρουν ώρες ή ακόμα και ημέρες.
5. Τα καλά σχεδιασμένα σουντόκου έχουν μια μοναδική λύση, χρησιμοποιήστε αυτό το χαρακτηριστικό προς όφελός σας.
6. Ποτέ μην μαντέψετε πριν εξετάσετε προσεκτικά όλες τις πιθανές κινήσεις.
7. Ακολουθήστε μια σειρά:Στην τοποθέτηση των αριθμών, μια καλή τακτική είναι να ξεκινήσετε με τους αριθμούς που εμφανίζονται συχνότερα, καταλήγοντας στους λιγότερο συχνούς. Σε περίπτωση ισοπαλίας, αποφασίστε τη σειρά και ακολουθήστε την καθ' όλη τη διάρκεια του παιχνιδιού.
8. Ελέγξτε ότι κάθε βήμα που κάνετε είναι έγκυρο, ένα λάθος στην αρχή μπορεί να είναι καταστροφικό.
9. Εάν δεν μπορείτε να βρείτε μια πιθανή λύση, ζητήστε βοήθεια ή δοκιμάστε το σουντόκου άλλη φορά. Συχνά η λύση εμφανίζεται όταν το περιμένετε λιγότερο, και όχι πάντα όταν βρίσκεστε μπροστά στο σουντόκου. 😉

Ο απλούστερος τρόπος για να ανακαλύψετε έναν αριθμό είναι όταν σε μια σειρά, στήλη ή τεταρτημόριο απομένει μόνο ένας αριθμός για τοποθέτηση. Σε αυτή την περίπτωση ο αριθμός που λείπει πηγαίνει στο μοναδικό κενό κελί.

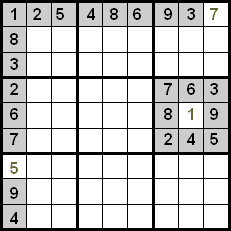
Όπως μπορείτε να δείτε, στην πρώτη σειρά έχουν τοποθετηθεί όλοι οι αριθμοί εκτός από το 7, οπότε στο κενό κελί μπορεί να πάει μόνο αυτός ο αριθμός. Στην πρώτη στήλη συμβαίνει κάτι παρόμοιο με το 5, όπως και στο έκτο τεταρτημόριο με το 1.

Ένας άλλος τρόπος για να ανακαλύψετε αριθμούς είναι να κάνετε μια διασταύρωση ανά σειρά και στήλη. Αυτό συνίσταται στο να εστιάσετε την προσοχή σε ένα κελί και να ελέγξετε ποιους αριθμούς μπορούν να πάνε σε αυτή τη θέση, εξαλείφοντας αυτούς που βρίσκονται στην ίδια σειρά ή στήλη.

Στην παρακάτω εικόνα μπορούμε να ελέγξουμε ότι στο υποδεικνυόμενο κελί μπορεί να πάει μόνο το 7, καθώς οι αριθμοί 1, 8, 3, 6 και 9 βρίσκονται στην ίδια στήλη και οι αριθμοί 2, 4 και 5 στην ίδια σειρά.

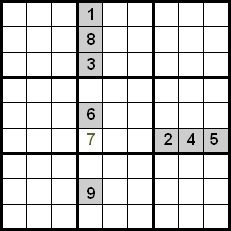
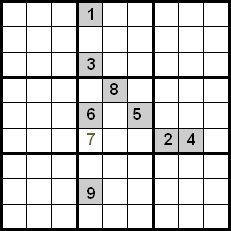
Μια βελτίωση αυτής της τεχνικής επιτυγχάνεται επίσης ελέγχοντας τους αριθμούς που βρίσκονται στο ίδιο τεταρτημόριο. Στο παρακάτω παράδειγμα μπορούμε να δούμε ότι χρησιμοποιώντας τη διασταύρωση μεταξύ σειρών και στηλών θα είχαμε ως υποψηφίους τους αριθμούς 5, 7 και 8 για να τους τοποθετήσουμε στο επισημασμένο κελί. Δεδομένου ότι οι αριθμοί 5 και 8 έχουν ήδη τοποθετηθεί στις θέσεις τους εντός του τεταρτημορίου, μπορούμε να τους απορρίψουμε, οπότε ο αριθμός 7 είναι αυτός που καταλαμβάνει την υποδεικνυόμενη θέση.

Η τεχνική του Ξιφία χρησιμοποιείται στα σουντόκου όταν ένας συγκεκριμένος αριθμός εμφανίζεται ως πιθανός σε ακριβώς τρεις σειρές και τρεις στήλες.

Αυτή η μέθοδος είναι ιδιαίτερα χρήσιμη για την απεμπλοκή αδιέξοδων καταστάσεων σε ένα προχωρημένο παιχνίδι. Σε μια πρακτική περίπτωση, εάν παρατηρήσετε ότι στις σειρές 1, 4 και 7, ο αριθμός 5 μπορεί να πάει μόνο στις ίδιες τρεις στήλες, έχετε αναγνωρίσει έναν Ξιφία. Τώρα μπορείτε να αφαιρέσετε με ασφάλεια τον αριθμό 5 από τις στήλες 2, 5 και 8 σε όλες τις άλλες σειρές, κάτι που συχνά καθαρίζει πολλά κελιά και διευκολύνει την επίλυση του υπόλοιπου σουντόκου.

Η XYZ-Πτέρυγα επικεντρώνεται στην εύρεση τριών κελιών που σχηματίζουν μια σύνδεση, όπου δύο έχουν δύο πιθανούς αριθμούς και το τρίτο (άξονας) μοιράζεται έναν αριθμό με καθένα από τα άλλα δύο.

Στην πράξη, εάν βρείτε αυτή τη διαμόρφωση σε ένα παιχνίδι σουντόκου, ανοίγει μια ευκαιρία για να μειώσετε σημαντικά τις πιθανότητες. Εφαρμόζοντας την τεχνική XYZ-Πτέρυγα, μπορείτε να εξαλείψετε επιλογές στρατηγικά, διευκολύνοντας την επίλυση των πιο πολύπλοκων τμημάτων του παζλ.

Η τεχνική της διπλής σύνδεσης εφαρμόζεται όταν δύο αριθμοί μπορούν να πάνε μόνο σε δύο κελιά μιας σειράς, στήλης ή μπλοκ, και αυτά τα κελιά δεν περιέχουν άλλους αριθμούς.

Φανταστείτε ένα σουντόκου όπου σε μια συγκεκριμένη σειρά, μόνο τα κελιά A2 και A8 μπορούν να περιέχουν τους αριθμούς 3 και 7. Εάν λύσουμε ότι το A2 πρέπει να περιέχει το 3, γνωρίζουμε αυτόματα ότι το A8 πρέπει να περιέχει το 7.

Η τεχνική μείωσης γραμμής-πλαισίου είναι μια προηγμένη στρατηγική που χρησιμοποιείται όταν οι πιθανές θέσεις ενός αριθμού σε μια σειρά ή στήλη βρίσκονται εξ ολοκλήρου μέσα σε μια ενιαία περιοχή ή πλαίσιο.

Για παράδειγμα, εάν σε ένα άνω πλαίσιο οι αριθμοί 4 μπορούν να εμφανιστούν μόνο σε κελιά που αποτελούν μέρος της σειράς 2, τότε μπορείτε να εξαλείψετε το 4 ως πιθανότητα στα άλλα κελιά αυτού του πλαισίου. Αυτή η τεχνική βελτιώνει την αποτελεσματικότητα κατά την επίλυση σύνθετων σουντόκου.